The Rules of Divisibility
Lessons with videos, examples, solutions and stories to help students learn the Divisibility Rules.
Related Pages
Basic Divisibility Rules
Divisibility Rules Explained
More Lessons for Arithmetic
Free Math Worksheets
The multiple of a number is always divisible by the number. The word “divisible” means that it can be divided exactly.
Example:
144 ÷ 4 = 36 (remainder = 0). So, 144 is divisible by 4 and is a multiple of 4.
144 ÷ 5 = 28 (remainder = 4). So, 144 is not divisible by 5 and is not a multiple of 5.
What are the Divisibility Rules?
The following table gives criteria or conditions to test divisibility of any number
by the numbers listed in the first column. This is useful when testing the divisibility
of large numbers and to determine whether a number is a multiple of another.
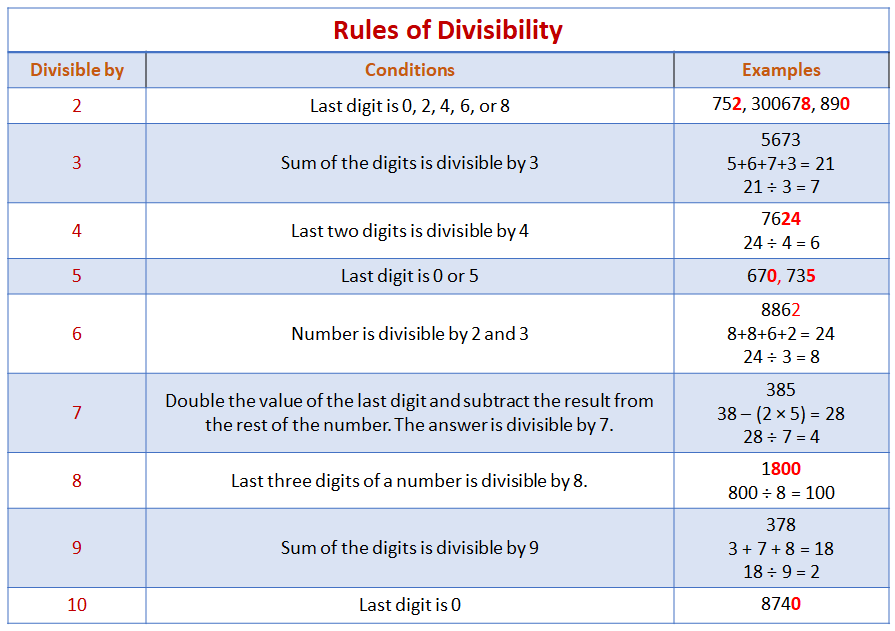
A number is divisible by 2 if its last digit is 0, 2, 4, 6 or 8.
A number is divisible by 3 if the sum of all its digits is divisible by 3.
A number is divisible by 4 if its last two digits is divisible by 4.
A number is divisible by 5 if its last digit is 0 or 5.
A number is divisible by 6 if it is divisible by 2 and 3.
A number is divisible by 7 if we double the value of the last digit and subtract the result from the rest of the number. The answer is divisible by 7.
A number is divisible by 8 if its last three digits is divisible by 8.
A number is divisible by 9 if the sum of all its digits is divisible by 9.
A number is divisible by 10 if its last digit is 0.
Example:
Check whether 171 is a multiple of 9.
Solution:
Sum of digits 1 + 7 + 1 = 9
9 ÷ 9 = 1
So, 171 is a multiple of 9
The following video describes the rules of divisibility.
A song to help you remember the divisibility rules.
Try out our new and fun Fraction Concoction Game.
Add and subtract fractions to make exciting fraction concoctions following a recipe. There are four levels of difficulty: Easy, medium, hard and insane. Practice the basics of fraction addition and subtraction or challenge yourself with the insane level.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.