Illustrative Mathematics Grade 8, Unit 5, Lesson 7: Connecting Representations of Functions

Related Pages
Illustrative Math
Grade 8

Lesson 7: Connecting Representations of Functions

Let’s connect tables, equations, graphs, and stories of functions.

Illustrative Math Unit 8.5, Lesson 7 (printable worksheets)

Lesson 7 Summary

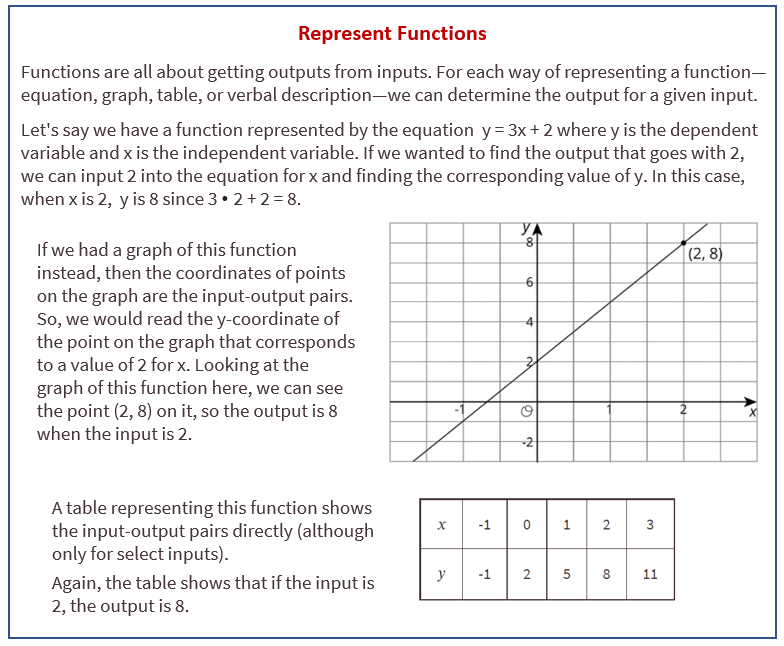
The following diagram shows how to compare inputs and outputs of functions that are represented in different ways.

Lesson 7.1 Which are the Same? Which are Different?

Here are three different ways of representing functions. How are they alike? How are they different?

• See Video for Whole Lesson

Lesson 7.2 Comparing Temperatures

The graph shows the temperature between noon and midnight in City A on a certain day.
The table shows the temperature, T, in degrees Fahrenheit, for h hours after noon, in City B.

1. Which city was warmer at 4:00 p.m.?
2. Which city had a bigger change in temperature between 1:00 p.m. and 5:00 p.m.?
3. How much greater was the highest recorded temperature in City B than the highest recorded temperature in City A during this time?
4. Compare the outputs of the functions when the input is 3.

Lesson 7.3 Comparing Volumes

The volume, V, of a cube with side length is given by the equation V = s³. The graph of the volume of a sphere as a function of its radius is shown.

1. Is the volume of a cube with side length s = 3 greater or less than a sphere with radius 3?
2. Estimate the radius of a sphere that has the same volume as a cube with side length 5.
3. Compare the outputs of the two volume functions when the inputs are 2. Here is an applet to use if you choose. Note: If you want to graph an equation with this applet, it expects you to enter y as a function of x, so you need to use y instead of V and x instead of s. Open Applet

Are you ready for more?

Estimate the edge length of a cube that has the same volume as a sphere with radius 2.5.

Lesson 7.4 It’s Not a Race

Elena’s family is driving on the freeway at 55 miles per hour.
Andre’s family is driving on the same freeway, but not at a constant speed. The table shows how far Andre’s family has traveled, d, in miles, every minute for 10 minutes.

1. How many miles per minute is 55 miles per hour?
2. Who had traveled farther after 5 minutes? After 10 minutes?
3. How long did it take Elena’s family to travel as far as Andre’s family had traveled after 8 minutes?
4. For both families, the distance in miles is a function of time in minutes. Compare the outputs of these functions when the input is 3.

Lesson 7 Practice Problems

1. The equation and the tables represent two different functions. Use the equation b = 4a - 5 and the table to answer the questions. This table represents c as a function of a.
2. Match each function rule with the value that could not be a possible input for that function.
3. Elena and Lin are training for a race. Elena runs her mile a constant speed of 7.5 miles per hour.
   Lin’s times are recorded every minute:
   a. Who finished their mile first?
   b. This is a graph of Lin’s progress. Draw a graph to represent Elena’s mile on the same axes.
   c. For these models, is distance a function of time? Is time a function of distance? Explain how you know.
4. Find a value of x that makes the equation true:

The Open Up Resources math curriculum is free to download from the Open Up Resources website and is also available from Illustrative Mathematics.

Try the free Mathway calculator and problem solver below to practice various math topics. Try the given examples, or type in your own problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.