Relations And Functions

Ordered-Pair Numbers

An ordered-pair number is a pair of numbers where the order in which they appear is significant. It is typically written in parentheses with the numbers separated by a comma, like (x,y).

For example, (4, 7) is an ordered-pair number; the order is designated by the first element 4 and the second element 7. The pair (7, 4) is not the same as (4, 7) because of the different ordering. Sets of ordered-pair numbers can represent relations or functions.

Relations Vs Functions
Relations	Functions	Vertical Line Test

Relations

A relation is any set of ordered-pair numbers. It describes a connection or relationship between elements from two sets. The set of all first components (or x-values) of the ordered pairs in a relation is called the domain of the relation. The set of all second components (or y-values) of the ordered pairs in a relation is called the range of the relation.

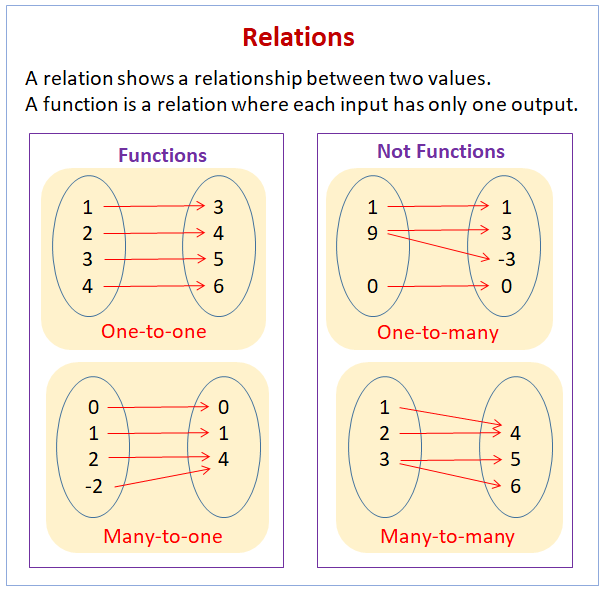
The following diagram shows some examples of relations and functions. Scroll down the page for more examples and solutions on how to determine if a relation is a function.

Suppose the weights of four students are shown in the following table.

Student	1	2	3	4
Weight	120	100	150	130

The pairing of the student number and his corresponding weight is a relation and can be written as a set of ordered-pair numbers.
W = {(1, 120), (2, 100), (3, 150), (4, 130)}

The set of all first elements is called the domain of the relation.
The domain of W = {1, 2, 3, 4}

The set of second elements is called the range of the relation.
The range of W = {120, 100, 150, 130}

Functions

A function is a special type of relation where each input (element from the domain) is assigned to exactly one output (element from the range). In other words, for every x-value, there is only one corresponding y-value. This is the defining characteristic of a function. Each input “maps” to precisely one output.

Example:
Determine whether the following are functions
a) A = {(1, 2), (2, 3), (3, 4), (4, 5)}
b) B = {(1, 3), (0, 3), (2, 1), (4, 2)}
c) C = {(1, 6), (2, 5), (1, 9), (4, 3)}

Solution:
a) A = {(1, 2), (2, 3), (3, 4), (4, 5)} is a function because all the first elements are different.

b) B = {(1, 3), (0, 3), (2, 1), (4, 2)} is a function because all the first elements are different. (The second element does not need to be unique)

c) C = {(1, 6), (2, 5), (1, 9), (4, 3)} is not a function because the first element, 1, is repeated.

How to Identify a Function:
1. From Ordered Pairs: Check if any x-value (first component) is repeated with different y-values (second components). If not, it’s a function.
2. From a Table: Similar to ordered pairs, look for repeated inputs with different outputs.
3. From a Graph (Vertical Line Test): If any vertical line drawn through the graph cuts the graph at more than one point, then the relation is not a function. This is called the vertical line test.

Videos

Determining Whether A Relation Is A Function

Understanding relations (defined as a set of inputs and corresponding outputs) is an important step to learning what makes a function. A function is a specific relation, and determining whether a relation is a function is a skill necessary for knowing what we can graph. Determining whether a relation is a function involves making sure that for every input there is only one output.

How To Determine If A Relation Is A Function?

A function is a correspondence between a first set, called the domain, and a second set, called the range, such that each member of the domain corresponds to exactly one member of the range.

The graph of a function f is a drawing hat represents all the input-output pairs, (x, f(x)). In cases where the function is given by an equation, the graph of a function is the graph of the equation y = f(x).

The vertical line test - a graph represents a function if it is impossible to draw a vertical line that intersects the graph more than once.

• Show Video Lesson

How To Determine If A Relation Is A Function?

This Algebra 1 level math video tutorial

• defines a relation as a set of ordered pairs and a function as a relation with one to one correspondence.
• models how to determine if a relation is a function with two different methods.
• shows how to use a mapping and the vertical line test.
• discusses how to work with function notation. It is defined as replacing y in an equation that is a function.

Examples:

1. Using a mapping diagram, determine whether each relation is a function.
2. Using a vertical line test, determine whether the relation is a function.
3. Make a table for f(t) = 0.5x + 1. Use 1, 2, 3, and 4 as domain values.
4. Evaluate the function rule f(g) = -2g + 4 to find the range for the domain (-1, 3, 5).

• Show Video Lesson

Determine If A Relation Is A Function

This video explains the concepts behind mapping a relation and the vertical line test.

• Show Video Lesson

Relations And Functions

• Show Video Lesson

Try out our new and fun Fraction Concoction Game.

Add and subtract fractions to make exciting fraction concoctions following a recipe. There are four levels of difficulty: Easy, medium, hard and insane. Practice the basics of fraction addition and subtraction or challenge yourself with the insane level.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.