Reciprocal of a Function
Related Topics:
More Lessons for PreCalculus
Math Worksheets
Examples, solutions, videos, worksheets, games, and activities to help PreCalculus students learn about the reciprocal of a function.
Reciprocal Transformation
One important concept in the study of polynomials is the reciprocal transformation. What happens when we take the reciprocal transformation of a function, or one over the function? Specifically, there are ways to create the graph of the reciprocal transformation of a function from the graph of the function itself. The reciprocal transformation is important in the definition of rational functions.
How to graph the reciprocal of a linear function?
When you graph the reciprocal of a linear function, \(f(x) = ax + b\), the resulting graph will be a hyperbola with specific characteristics determined by the original linear function. The reciprocal function is given by \(g(x) = \frac{1}{ax + b}\).
The following diagram shows how to graph the reciprocal of a linear function. Scroll down the page for more examples and solutions on graphing reciprocal functions.
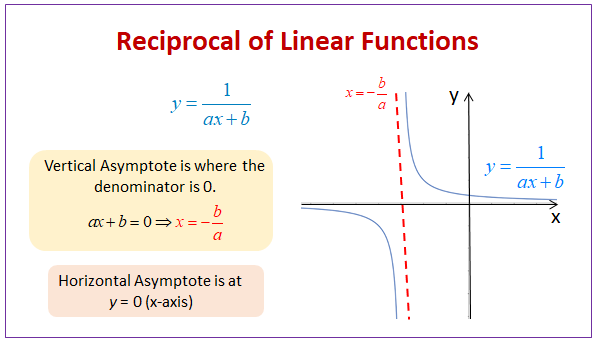
Steps to graphing the reciprocal of a linear function
- Identify the Vertical Asymptote:
The vertical asymptote occurs where the denominator of the reciprocal function equals zero.
Set the linear function equal to zero and solve for \(x\): \(ax + b = 0 \implies x = -\frac{b}{a}\)
The vertical asymptote is \(x = -\frac{b}{a}\) - Identify the Horizontal Asymptote:
As \(|x|\) becomes very large (approaches infinity), the term \(\frac{1}{ax + b}\) approaches 0.
The horizontal asymptote is \(y = 0\). There is no x-intercept. - Find the y-intercept:
Set \(x = 0\) in the reciprocal function: \(g(0) = \frac{1}{a(0) + b} = \frac{1}{b}\)
The y-intercept is at the point \((0, \frac{1}{b})\), provided \(b \neq 0\). If \(b = 0\), there is no y-intercept because the vertical asymptote is the y-axis. - Sketch the two branches of the hyperbola, ensuring they approach the asymptotes but do not cross them.
How to graph the reciprocal of a linear function?
Graphing Reciprocal Functions (Considering sign)
Graphing Reciprocal Functions (Considering symmetry)
Graphing Reciprocal Functions (Cubic + semi-circle examples)
Reciprocal of a Linear Function Part 1
This lesson is about the reciprocal of a linear function and discusses domain and range, along with behavior near both vertical and horizontal asymptotes. This is the first part of a two part lesson.
Reciprocal of a Linear Function Part 2
Reciprocal of a Function - part 1
Reciprocal of a Function - part 2
Reciprocal of a Function - part 3
Try out our new and fun Fraction Concoction Game.
Add and subtract fractions to make exciting fraction concoctions following a recipe. There are four levels of difficulty: Easy, medium, hard and insane. Practice the basics of fraction addition and subtraction or challenge yourself with the insane level.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.