OML Search

Illustrative Mathematics Unit 6.1, Lesson 3: Reasoning to Find Area

Related Topics:
Math Worksheets




Learn more about finding the area of shapes by decomposing and rearranging them into regular shapes, with or without grids. After trying the questions, click on the buttons to view answers and explanations in text or video.

Return to the list of Illustrative Math lessons


Reasoning to Find Area
Let’s decompose and rearrange shapes to find their areas.

Illustrative Math Unit 6.1, Lesson 3 (printable worksheets)

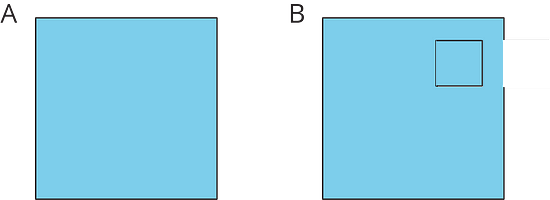
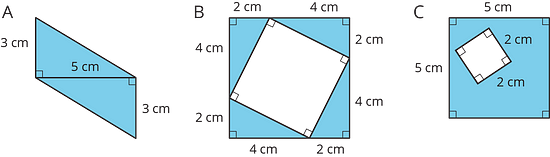
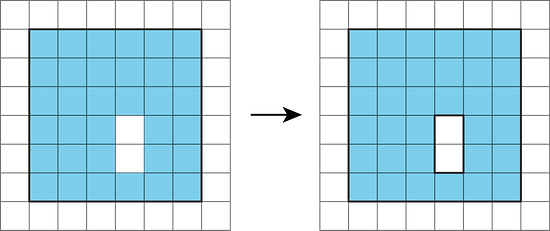
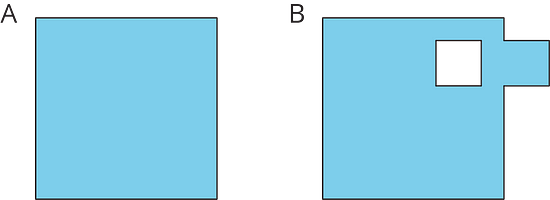
3.1 - Comparing Regions

Is the area of Figure A greater than, less than, or equal to the area of the shaded region in Figure B? Be prepared to explain your reasoning.

Square A, shaded. Square B identical to A, with a small shaded square removed in the middle and a small shaded square appended to its side.

  • Hints

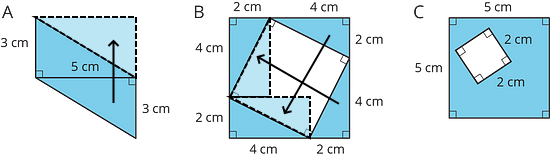
    Recall the strategies used in the previous lesson, such as decomposing and rearranging figures, and comparing figures.

  • Answers

    Square A, shaded. Square B identical to A. A small shaded square previously appended to the side of Figure B has been placed in a previously empty space within Figure B.

    The area of Figure A is equal to the area of the shaded region in Figure B. The shaded region of Figure B can be decomposed and rearranged into a figure that matches Figure A exactly.

  • See Video 1 for Whole Lesson
  • See Video 2 for Whole Lesson




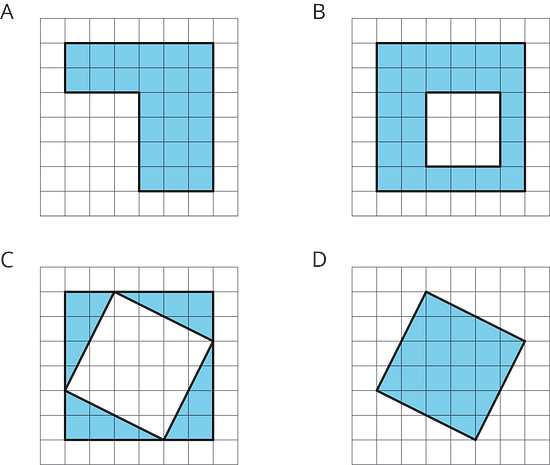
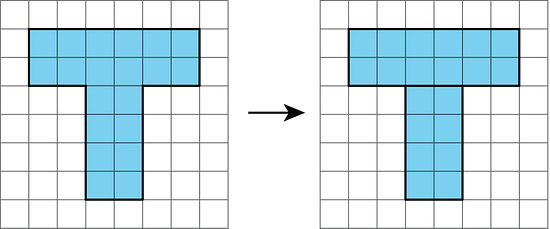
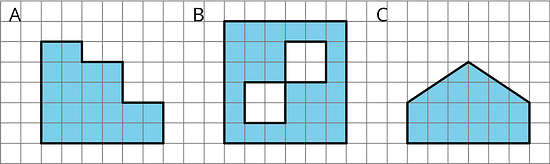
3.2 - On the Grid

Each grid square is 1 square unit. Find the area, in square units, of each shaded region without counting every square. Be prepared to explain your reasoning.

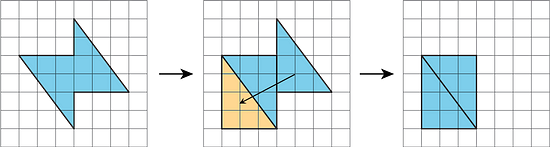
Rearrange the triangles from Figure C so they fit inside Figure D. Draw and color a diagram of your work on the grid.

  • See Possible Answers

    Four figures, each on a white square grid. Figure A is a green corner piece with 6 sides. Figure B a 6 by 6 green square with a 3 by 3 white square inside. Figure C a 6 by 6 green square with a tilted white square inside. Figure D is a green tilted square. The figures have been labelled with the lengths of their sides to help in finding the area of each figure. Figure C has been decomposed and rearranged into 2 rectangles with dimensions 2 by 4 each. Figure D has been rearranged into 2 rectangles with dimensions 2 by 4 each, plus a square 2 by 2 in the middle.

    Each figure can be decomposed and rearranged into regular shapes whose areas can be added or subtracted to find the total area of each figure.

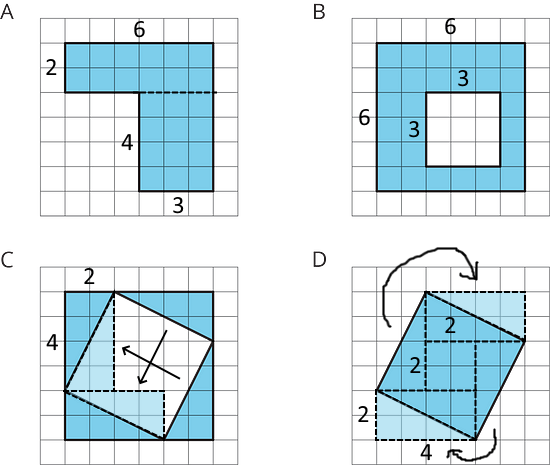
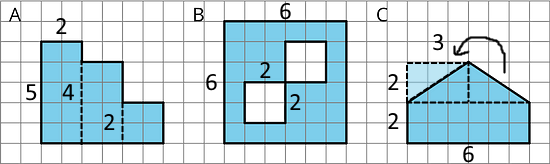
    Figure A can be decomposed into 2 rectangles, one with an area of 2 × 6 = 12 square units and the other with an area of 4 × 3 = 12 square units. Hence, the total area of Figure A is 12 + 12 = 24 square units. You can count the squares to check your answer.

    Figure B has an area of 6 × 6 = 36 square units, minus the unshaded region in the middle which has an area of 3 × 3 = 9 square units. Hence, the total area of Figure B is 36 - 9 = 27 square units. Just as regular parts of figures can be added together, regular shapes which are not included in a figure's area can be subtracted.

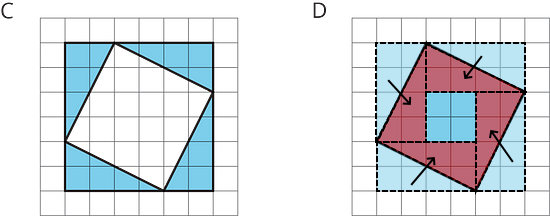
    Figure C consists of 4 right triangles, which can be rearranged into 2 rectangles with areas 2 × 4 = 8 square units each. Hence, the total area of Figure C is 2 × 8 = 16 square units.

    Figure D can be decomposed into 4 right triangles and a square. Like in Figure C, the 4 right triangles can be rearranged into 2 rectangles with areas 2 × 4 = 8 square units each. The total area of the 2 rectangles is 2 × 8 = 16 square units. The area of the square is 2 × 2 = 4 square units. Hence, the total area of Figure D is 16 + 4 = 20 square units.

    Two figures, each on a white square grid. Figure C a 6 by 6 green square with a tilted white square inside. Figure D is a green tilted square. The triangles from Figure C have been overlaid onto Figure D.
    The triangles from Figure C have been overlaid onto Figure D in blue with dashed outlines, and then rearranged to fit inside Figure D (red triangles with dashed outlines).




3.3 - Off the Grid

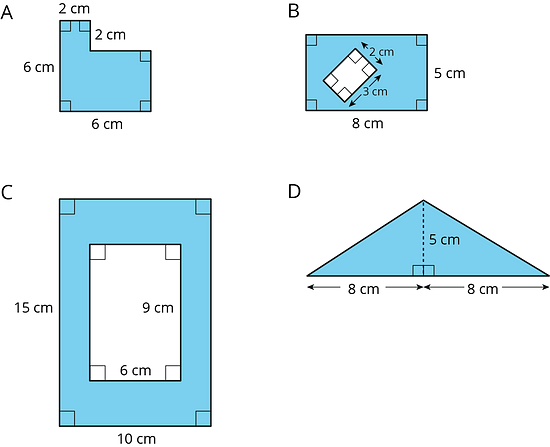
Find the area of the shaded region(s) of each figure. Explain or show your reasoning.

  • See Possible Answers

    Three figures. Figure A is two right triangles which both have heights of 3 cm and bases of 5 cm. These have been rearranged to make a rectangle. Figure B is a 6 by 6 cm blue square with a tilted white square inside. Figure B has been decomposed and rearranged to make 2 rectangles with dimensions 2 by 4 cm each. Figure C is a 5 by 5 cm blue square with a tilted 2 by 2 cm white square inside.

    Similar to the previous problem, each figure can be decomposed and rearranged into regular shapes whose areas can be added or subtracted to find the total area of each figure. This can be done without a grid.

    Figure A consists of 2 right triangles, can be rearranged into a rectangle that is 3 cm by 5 cm. The area of this rectangle, and therefore the area of Figure A, is 3 × 5 = 15 square centimeters.

    Figure B consists of 4 right triangles, which can be rearranged into 2 rectangles that are 2 cm by 4 cm each. The area of these 2 rectangles, and therefore the area of Figure B, is 2 × 2 × 4 = 16 square centimeters.

    Figure C has an area of 5 × 5 = 25 square centimeters, minus the unshaded region in the middle which has an area of 2 × 2 = 4 square centimeters. Hence, the total area of Figure C is 25 - 4 = 21 square centimeters.


Lesson 3 Summary

There are different strategies we can use to find the area of a region. We can:

  • Decompose it into shapes whose areas you know how to calculate; find the area of each of those shapes, and then add the areas.

    Two images of a t-shaped object. The upper portion is 2 units tall and 6 units wide. The stem of the “t” is 4 units tall and 2 units wide. The second image is the same, except there is a line separating the upper portion and lower portion into two rectangles.

  • Decompose it and rearrange the pieces into shapes whose areas you know how to calculate; find the area of each of those shapes, and then add the areas.

    Images showing an irregular shape being decomposed into two right triangles, which is then rearranged to make one rectangle.

  • Consider it as a shape with a missing piece; calculate the area of the shape and the missing piece, and then subtract the area of the piece from the area of the shape.

    Two shaded squares in a grid. Each are 6 units square and each as a 1 unit by two unit portion that is unshaded.

The area of a figure is always measured in square units. When both side lengths of a rectangle are given in centimeters, then the area is given in square centimeters.

The area of this rectangle is 32 square centimeters.


Practice Problems

1. Find the area of each shaded region. Show your reasoning.

  • See Possible Answers

    Three figures. Figure A resembles a staircase. Figure B is a blue square with two white squares in the middle. Figure C has 5 sides, 2 sloping sides and 3 sides which form right angles with each other. Each has been decomposed and rearranged into regular shapes.

    Figure A can be decomposed into 3 rectangles. One example is shown. The total area of Figure A is (2 × 5) + (2 × 4) + (2 × 2) = 20 square units.

    Figure B consists of a square with an area of 6 × 6 = 36 square units, minus 2 squares with a total area of 2 × (2 &215; 2) = 8 square units. Figure B has an area of 36 - 8 = 28 square units.

    Figure C can be decomposed into 1 rectangle and 2 right triangles. The right triangles can be rearranged into 1 rectangle as shown. The area of this new rectangle is 3 × 2 = 6 square units. The area of the rectangle at the bottom is 2 × 6 = 12 square units. The total area of Figure C is 6 + 12 = 18 square units.


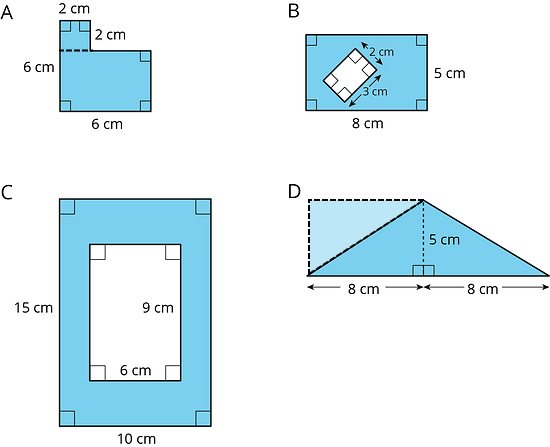
2. Find the area of each shaded region. Show or explain your reasoning.

  • See Possible Answers

    Four figures. Figure A is a square 6 cm by 6 cm, with a smaller square 2 cm by 2 cm appended to its top. Figure B is a rectangle 5 cm by 8 cm, with a tilted white rectangle 2 cm by 3 cm inside it. Figure C is a rectangle 15 cm by 10 cm, with a white rectangle 9 cm by 6 cm inside it. Figure D is two right triangles. Each triangle has a base of 8 cm and a height of 5 cm. Figure D has been rearranged to form a rectangle.

    Figure A can be decomposed into 2 squares. The total area of Figure A is (2 × 2) + (6 × 6) = 40 square cm.

    Figure B consists of a rectangle 5 cm by 8 cm, minus a smaller unshaded rectangular piece 2 cm by 3 cm. The total area of Figure B is (5 × 8) + (2 × 3) = 34 square cm.

    Figure C consists of a rectangle 15 cm by 10 cm, minus a smaller unshaded rectangle 9 cm by 6 cm. The total area of Figure C is (15 × 10) + (9 × 6) = 96 square cm.


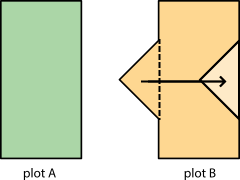
3. Two plots of land have very different shapes. Noah said that both plots of land have the same area.

Do you agree with Noah? Explain your reasoning.

  • Answers

    Two shapes labeled “plot A” and “plot B”. Plot “A” is a rectangle and plot “B” is the same height, but has a triangular shape removed from the right side, and an identical triangle shape added to the left side. The triangular shape has been moved back to the right side.

    Both plots of land have the same area. Plot B can be decomposed and rearranged into a rectangle identical to Plot A. Therefore, Plot B has the same area as Plot A.


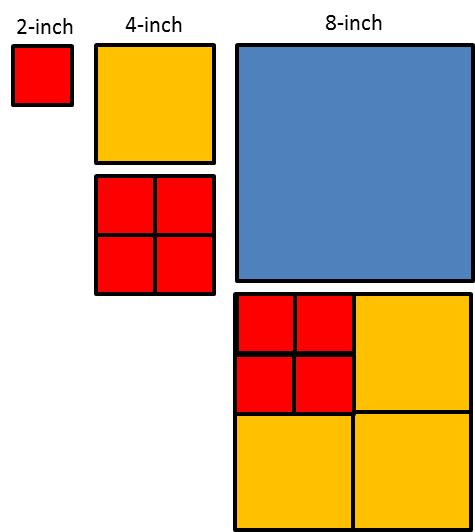
4. A homeowner is deciding on the size of tiles to use to fully tile a rectangular wall in her bathroom that is 80 inches by 40 inches. The tiles are squares and come in three side lengths: 8 inches, 4 inches, and 2 inches. State if you agree with each statement about the tiles. Explain your reasoning.

A. Regardless of the size she chooses, she will need the same number of tiles.
B. Regardless of the size she chooses, the area of the wall that is being tiled is the same.
C. She will need two 2-inch tiles to cover the same area as one 4-inch tile.
D. She will need four 4-inch tiles to cover the same area as one 8-inch tile.
E. If she chooses the 8-inch tiles, she will need a quarter as many tiles as she would with 2-inch tiles.

  • Answers

    We can visually compare the area covered by each type of tile, as well as calculate the area covered using the side lengths.

    A comparison of squares representing square tiles which are 2 square inches, 4 square inches, and 8 square inches. Four 2-inch tiles cover the same area as a 4-inch tile, and four 4-inch tiles cover the same area as an 8-inch tile.

    A is false. The different sizes of tiles will cover different areas per tile. Larger tiles cover a larger area, so fewer tiles will be needed to cover a given area of wall compared to smaller tiles.

    B is true. The area of wall to be tiled does not depend on the size of the tiles being used.

    C is false. One 4-inch tile has an area of 4 × 4 = 16 square inches. One 2-inch tile has an area of 2 × 2 = 4 square inches. Two 2-inch tiles have an area of 8 square inches, not 16 square inches. It takes four 2-inch tiles to cover the same area as a 4-inch tile.

    D is true. One 8-inch tile has an area of 8 × 8 = 64 square inches. One 4-inch tile has an area of 16 square inches. Four 4-inch tiles have an area of 4 × 16 = 64 square inches.

    E is false. One 8-inch tile has an area of 64 square inches. One 2-inch tile has an area of 4 square inches, which is 1⁄16 of an 8-inch tile, not ¼.



The Open Up Resources math curriculum is free to download from the Open Up Resources website and is also available from Illustrative Mathematics.

Try the free Mathway calculator and problem solver below to practice various math topics. Try the given examples, or type in your own problem and check your answer with the step-by-step explanations.
Mathway Calculator Widget


OML Search


We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.



 
Back to Top | Interactive Zone | Home

Copyright © 2005, 2024 - OnlineMathLearning.com.
Embedded content, if any, are copyrights of their respective owners.