Rational Numbers
Related Topics:
More Lessons for Grade 6 Math
Math Worksheets
Videos, worksheets, solutions and songs to help Grade 6 students learn about rational numbers.
Rational Numbers
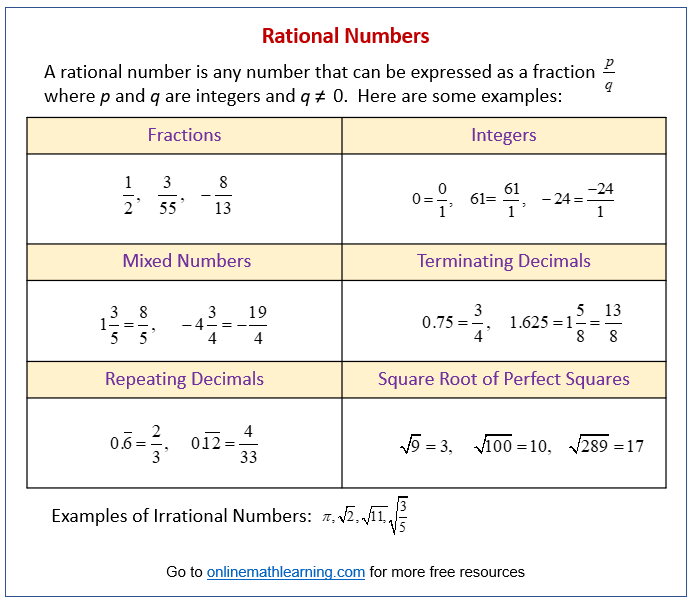
A rational number is any number that can be expressed as a fraction \( \frac{p}{q} \) where:
- \( p \) is an integer.
- \( q \) is an integer, but \( q \) cannot be zero.
The word “rational” comes from the word “ratio”. Essentially, a rational number is a ratio of two integers. The set of rational numbers is often denoted by the symbol Q.
The following diagram gives some examples of rational and irrational numbers. Scroll down the page for more examples and solutions.
Fraction, Decimal & Rational Number Worksheets
Practice your skills with the following worksheets:
Online & Printable Fraction Worksheets
Online & Printable Decimal Worksheets
Online & Printable Rational Number Worksheets
Examples of Rational Numbers:
- Integers: All integers are rational numbers because they can be written as a fraction with a denominator of 1 (e.g., \(5 = \frac{5}{1}\), \(-3 = \frac{-3}{1}\), \(0 = \frac{0}{1}\)).
- Fractions: Any fraction where the numerator and denominator are integers (and the denominator is not zero) is a rational number1 (e.g., \(\frac{1}{2}\), \(\frac{-3}{4}\), \(\frac{7}{9}\)).
- Mixed Numbers: Mixed numbers can be converted into improper fractions, so they are also rational (e.g., \(2\frac{1}{3} = \frac{7}{3}\)).
- Terminating Decimals: The decimal ends after a finite number of digits (e.g., 0.5, 0.75, 2.345). These can always be written as a fraction (e.g., \(0.5 = \frac{1}{2} \), \(0.75 = \frac{3}{4} \), \(2.345 = \frac{2345}{1000} \)).
- Repeating Decimals: The decimal has a sequence of digits that repeats infinitely (e.g., 0.333…, 0.141414…). These can also be converted into fractions. (e.g., \(0.333… = \frac{1}{3} \) , \(0.141414… = \frac{14}{99} \)).
- Square Roots of Perfect Squares: The square root of a perfect square is an integer, which is rational (e.g., \(\sqrt{9} = 3 = \frac{3}{1}\), \(\sqrt{16} = 4 = \frac{4}{1}\)).
What are NOT Rational Numbers? (Irrational Numbers)
Numbers that cannot be expressed in the form \(\frac{p}{q}\) where \(p\) and \(q\) are integers and \(q \neq 0\) are called irrational numbers. Their decimal representations are non-terminating and non-repeating.
Examples of irrational numbers include:
\(\pi\) (pi) ≈ 3.14159… (non-terminating, non-repeating)
\(\sqrt{2}\) ≈ 1.41421… (non-terminating, non-repeating)
\(\sqrt{3}\) ≈ 1.73205… (non-terminating, non-repeating)
How to classify real numbers as rational or irrational?
Real Numbers are numbers that would appear on the number line.
Rational Numbers are numbers that can be written in the form a/b with a and b as integers (b ≠ 0). In decimal form they terminate or do not terminate and repeat.
Irrational numbers are numbers in decimal form that do not terminate and do not repeat.
Example:
Classify each number as rational or irrational.
3√27, π √27, 5.9, √81, 3√16
What are Rational Numbers?
Rational Numbers - Decimals, Fractions, Percents Three forms of rational numbers - Fractions, percents and decimals
Rational Numbers
Number Types Song - Natural Numbers, Whole Numbers, Integers, Rational Numbers
Natural numbers are naturally
Numbers you count on your hands and your feet
1, 2, 3, 4, 5, 6, and so on
Whole numbers are natural numbers plus zero
That’s the only difference, oh, oh
0, 1, 2, 3, and so on
Integers are whole numbers plus negatives
They look a little bit like this
-2, -1, 0, 1, and so on
Last but not least, not to be outdone
Rational numbers are integers plus fractions
Like -3, 1/2, 5/8 and 14.2
All natural numbers are whole numbers
All whole numbers are integers
All integers are rational numbers
Now listen to that drummer!
What about 4? It’s a natural number so it’s also whole, integer, and rational
What about -2? Integer and rational
What about 1.5? It’s just rational
What about 0? It’s whole, integer, and rational
All natural numbers are whole numbers
All whole numbers are integers
All integers are rational numbers
Now listen to that drummer!
Rational Number Song
A song about rational number and rules in adding signed numbers.
Try out our new and fun Fraction Concoction Game.
Add and subtract fractions to make exciting fraction concoctions following a recipe. There are four levels of difficulty: Easy, medium, hard and insane. Practice the basics of fraction addition and subtraction or challenge yourself with the insane level.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.