Quadratic Inequalities

Related Pages
Solving Quadratic Equations
Quadratic Inequalities 2
More Algebra Lessons

Example:
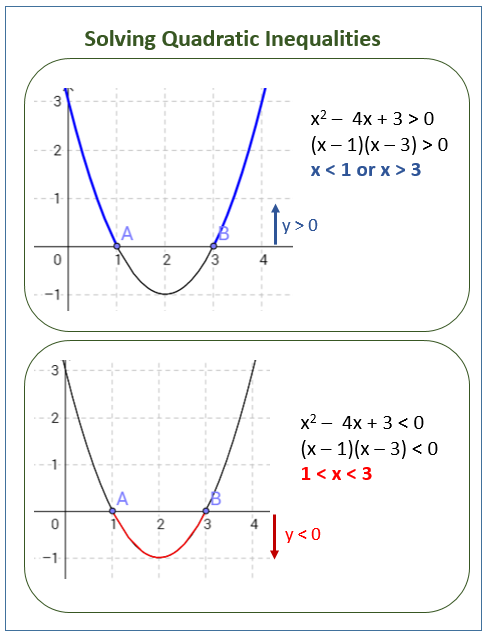
Solve the quadratic inequality x² – 4x > –3

Solution:
Step 1: Make one side of the inequality zero
x² – 4x > –3
x² – 4x + 3 > 0

Step 2: Factor the quadratic expression
x² – 4x + 3 > 0
(x – 3)(x – 1) > 0

Step 3: Find the range of values of x which satisfies the inequality.
(x – 3)(x – 1) > 0 (y is positive): we choose the interval for which the curve is above the x-axis.
x < 1 or x > 3

Note: If the quadratic inequality was (x – 3)(x – 1) < 0 (y is negative), we would have chosen the interval for which the curve is below the x-axis i.e. 1 < x < 3

The following graphs show the solutions for x² – 4x + 3 > 0 and x² – 4x + 3 < 0. Scroll down the page for more examples and solutions.

Example:
Solve 2x² < 9x + 5

Solution:
Step 1: Make one side of the inequality zero
2x² < 9x + 5
2x² – 9x – 5 < 0

Step 2: Factor the quadratic expression
2x² – 9x – 5 < 0
(2x + 1)(x – 5) < 0

Step 3: Find the range of values of x which satisfies the inequality.
(2x + 1)(x – 5) < 0 (y is negative): we choose the interval for which the curve is below the x-axis.

Note: If the quadratic inequality was (2x + 1)(x – 5) > 0 (y is positive) we would have chosen the interval for which the curve is above the x-axis i.e. or x > 5

How to solve quadratic inequalities?

Guidelines for solving Quadratic Inequalities

1. Find all the zeros of the polynomial, and arrange the zeros in increasing order. The zeros are called its critical numbers.
2. Plot those numbers on the number line as open or closed points based upon the original inequality symbol.
3. Choose a test value in each interval to see if the interval satisfies the inequality or not. If the test value produces a true statement, the entire interval will be true. If the interval produces a false statement, the entire interval is false.
4. Clearly graph your solution and state the solution using interval notation or inequalities.

Examples:

1. Solve x² - 6x - 16 ≤ 0
2. Solve 2x² - 11x + 12 > 0
3. Solve x² + 4 > 0

• Show Video Lesson

Solve a Quadratic Inequality

Example:
x² - x - 12 ≤ 0

• Show Video Lesson

How to solve a Quadratic Inequality?

Example:
2x² + 3x - 5 > 0

• Show Video Lesson

Solving Quadratic Inequalities

1. Turn inequality into an equation.
2. Find solutions.
3. Make a number line, and check each solution and interval.

Example:
Solve x² + 2x - 8 ≥ 0

• Show Video Lesson

Solving Quadratic Inequalities - Step by step

Example:
Find all the solutions to
2x² + 5x - 12 ≥ 0

• Show Video Lesson

Solving Quadratic Inequalities

Example:
Find all the solutions to
2x² < -4x + 6

• Show Video Lesson

Try out our new and fun Fraction Concoction Game.

Add and subtract fractions to make exciting fraction concoctions following a recipe. There are four levels of difficulty: Easy, medium, hard and insane. Practice the basics of fraction addition and subtraction or challenge yourself with the insane level.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.