Solving Quadratic Equations
This lesson is part of a series of lessons for the quantitative reasoning section of the GRE revised General Test. In this lesson, we will learn:
- Quadratic Equations
- Solve Quadratic Equations using the Quadratic Formula
- Using the Discriminant to find the number of Solutions
- Solve Quadratic Equations by Factoring
Quadratic Equations
A quadratic equation in the variable x is an equation that can be written in the form
ax2 + bx + c = 0
where a, b, and c are real numbers and a ≠ 0.
When such an equation has solutions, they can be found using the quadratic formula:
where the notation ± is shorthand for indicating two solutions: one that uses the plus sign and the other that uses the minus sign.
Let us consider an example.
Find the solutions for the quadratic equation: 4x2 + 26x + 12 = 0
From the equation, we get a = 4, b = 26 and c = 12. Putting the values into the formula, we get
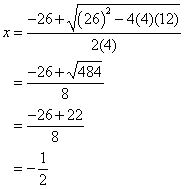
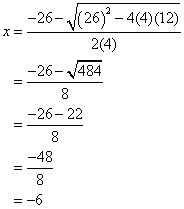Answer: :
The following video shows how to use the quadratic formula to find solutions to quadratic equations.
Using the Discriminant to find number of solutions
In the quadratic formula, the expression under the square root sign, which is b2 − 4ac, is called the discriminant of the quadratic equation.
Quadratic equations can have two real solutions, one real solution or no real solution. The number of solutions is determined by the discriminant.
If the discriminant is positive then there are two distinct solutions.
For example, in the quadratic equation 4x2 + 26x + 12 = 0, its discriminant is equals to b2 − 4ac = (26)2 − 4(4)(12) = 484 which is positive and so the equation has two real solutions.
If the discriminant is zero, then there is exactly one real solution.
For example, in the quadratic equation x2 + 4x + 4 = 0, its discriminant is equals to
b2 − 4ac = (4)2 − 4(1)(4) = 0 and so the equation has exactly one real solution.
If the discriminant is negative, then there is no real solution.
For example, in the quadratic equation x2 + x + 5 = 0, its discriminant is equals to
b2 − 4ac = (1)2 − 4(1)(5) = −19 which is negative and so the equation has no real solution.
The following videos show how to use discriminants to determine the number of real solutions to quadratic equations.
Solving Quadratic Equations by Factoring
Some quadratic equations can be solved more quickly by factoring. For example, the quadratic equation x2 + 7x + 10 = 0 can be factored as(x + 2) (x + 5) = 0
When a product is equal to 0, at least one of the factors must be equal to 0, which leads to two cases: x + 2 = 0 or x + 5 = 0
We then get two values for x.
The following video shows how to solve quadratic equations by factoring.
Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.