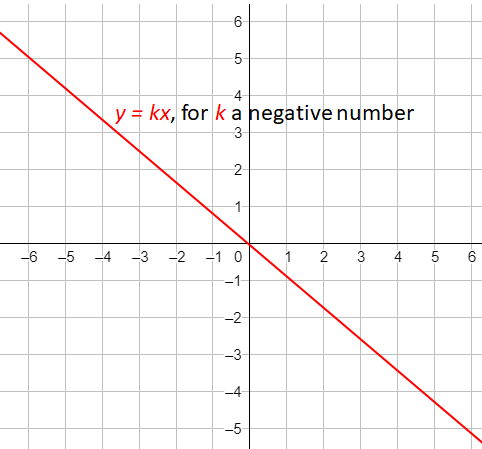Illustrative Mathematics Grade 7, Unit 2, Lesson 10: Introducing Graphs of Proportional Relationships

Related Pages
Illustrative Math
Grade 7

Lesson 10: Introducing Graphs of Proportional Relationships

Let’s see how graphs of proportional relationships differ from graphs of other relationships.

Illustrative Math Unit 7.2, Lesson 10 (printable worksheets)

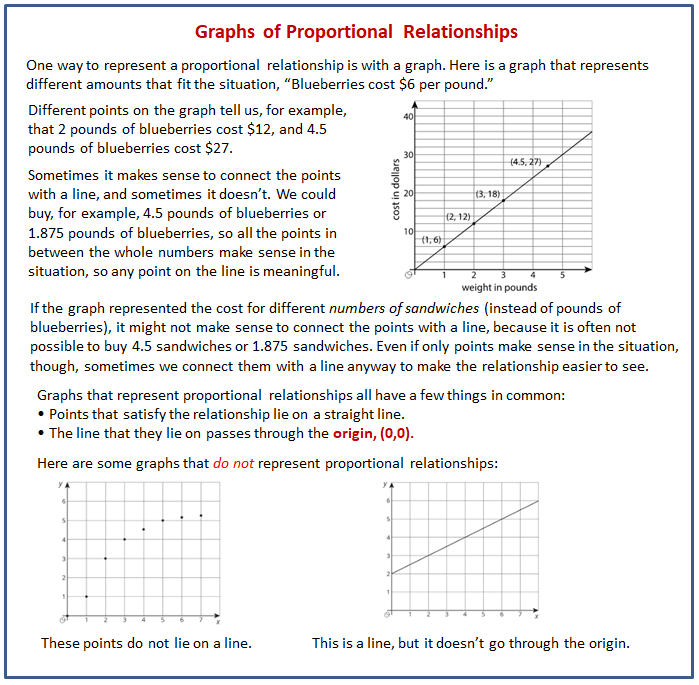
Lesson 10 Summary

The following diagram shows how graphs of proportional relationships differ from graphs of other relationships.

Lesson 10.1 Notice These Points

Plot the points. What do you notice about the graph?
(0,10),(1,8),(2,6),(3,4),(4,2)
Open Applet

• See Video for Whole Lesson

Lesson 10.2 T-shirts for Sale

Some T-shirts cost $8 each.

1. Use the table to answer these questions.
   a. What does x represent?
   b. What does y represent?
   c. Is there a proportional relationship between x and y?
   
2. Plot the pairs in the table on the coordinate plane.
   Open Applet
   
3. What do you notice about the graph?
   

Lesson 10.3 Matching Tables and Graphs

Your teacher will give you papers showing tables and graphs.

1. Examine the graphs closely. What is the same and what is different about the graphs?
2. Sort the graphs into categories of your choosing. Label each category. Be prepared to explain why you sorted the graphs the way you did.
3. Take turns with a partner to match a table with a graph.
   a. For each match you find, explain to your partner how you know it is a match.
   b. For each match your partner finds, listen carefully to their explanation. If you disagree, work to reach an agreement. Pause here so your teacher can review your work.
   
4. Trade places with another group. How are their categories the same as your group’s categories? How are they different?
5. Return to your original place. Discuss any changes you may wish to make to your categories based on what the other group did.
6. Which of the relationships are proportional?
7. What have you noticed about the graphs of proportional relationships? Do you think this will hold true for all graphs of proportional relationships?

Are you ready for more?

1. All the graphs in this activity show points where both coordinates are positive. Would it make sense for any of them to have one or more coordinates that are negative?
   • Show Answer

     For the examples in the lesson, it would not make sense for any of the coordinates to be negative.

2. The equation of a proportional relationship is of the form y = kx, where k is a positive number, and the graph is a line through (0,0). What would the graph look like if k were a negative number?
   • Show Answer

     

Lesson 10 Practice Problems

1. Which graphs could represent a proportional relationship? Explain how you decided.
   
2. A lemonade recipe calls for 1/4 cup of lemon juice for every cup of water.
   a. Use the table to answer these questions.
   i. What does x represent?
   ii. What does y represent?
   iii. Is there a proportional relationship between x and y?
   b. Plot the pairs in the table in a coordinate plane.
   
3. Decide whether each table could represent a proportional relationship. If the relationship could be proportional, what would be the constant of proportionality?
   a. The sizes you can print a photo:
   b. The distance from which a lighthouse is visible:
   
4. Select all of the pieces of information that would tell you x and y have a proportional relationship. Let y represent the distance between a rock and a turtle’s current position in meters and x represent the number of minutes the turtle has been moving.
   A. y = 3x
   B. After 4 minutes, the turtle has walked 12 feet away from the rock.
   C. The turtle walks for a bit, then stops for a minute before walking again.
   D. The turtle walks away from the rock at a constant rate.
   

The Open Up Resources math curriculum is free to download from the Open Up Resources website and is also available from Illustrative Mathematics.

Try the free Mathway calculator and problem solver below to practice various math topics. Try the given examples, or type in your own problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.