Illustrative Mathematics Grade 7, Unit 3, Lesson 1: How Well Can You Measure

Related Pages
Illustrative Math
Grade 7

Lesson 1: How Well Can You Measure?

Let’s see how accurately we can measure.

Illustrative Math Unit 7.3, Lesson 1 (printable worksheets)

Lesson 1 Summary

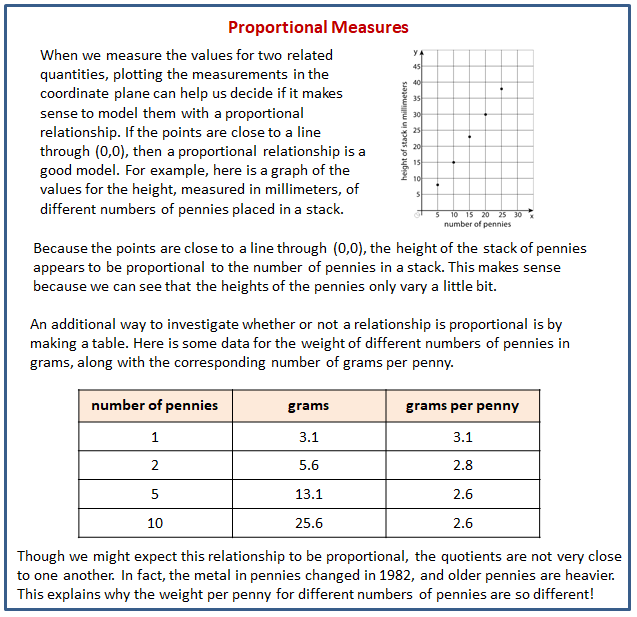
The following diagram shows how to use a graph to decide whether two associated quantities are in a proportional relationship.

Lesson 1.1 Estimating a Percentage

A student got 16 out of 21 questions correct on a quiz. Use mental estimation to answer these questions.

1. Did the student answer less than or more than 80% of the questions correctly?
2. Did the student answer less than or more than 75% of the questions correctly?
   

• See Video for Whole Lesson

Lesson 1.2 Perimeter of a Square

Here are nine squares.
Your teacher will assign your group three of these squares to examine more closely.

1. For each of your assigned squares, measure the length of the diagonal and the perimeter of the square in centimeters.
   Check your measurements with your group. After you come to an agreement, record your measurements in the table.
   
2. Plot the diagonal and perimeter values from the table on the coordinate plane.
   Open Applet
   
3. What do you notice about the points on the graph?

Lesson 1.3 Area of a Square

Andre and Jada were in a hot dog eating contest. Andre ate 10 hot dogs in 3 minutes. Jada ate 12 hot dogs in 5 minutes.

1. In the table, record the length of the diagonal for each of your assigned squares from the previous activity. Next, calculate the area of each of your squares.
   Pause here so your teacher can review your work. Be prepared to share your values with the class.
   
2. Examine the class graph of these values. What do you notice?
3. How is the relationship between the diagonal and area of a square the same as the relationship between the diagonal and perimeter of a square from the previous activity? How is it different?
   

Are you ready for more?

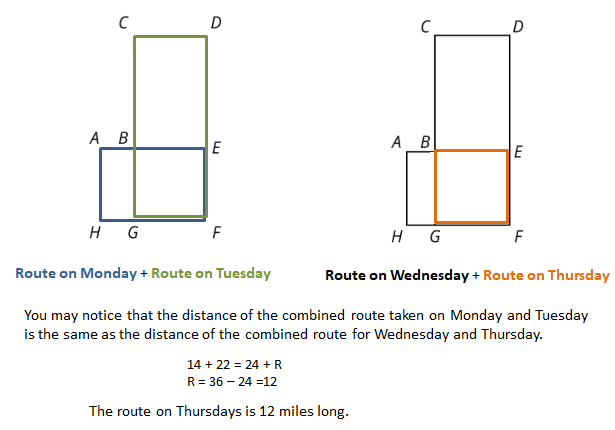
Here is a rough map of a neighborhood.
There are 4 mail routes during the week.
On Monday, the mail truck follows the route A-B-E-F-G-H-A, which is 14 miles long.
On Tuesday, the mail truck follows the route B-C-D-E-F-G-B, which is 22 miles long.
On Wednesday, the truck follows the route A-B-C-D-E-F-G-H-A, which is 24 miles long.
On Thursday, the mail truck follows the route B-E-F-G-B.
How long is the route on Thursdays?

• Show Answer

  

Lesson 1 Practice Problems

1. Estimate the side length of a square that has a 9 cm long diagonal.
   
2. Select all quantities that are proportional to the diagonal length of a square.
   A. Area of a square
   B. Perimeter of a square
   C. Side length of a square
   
3. Diego made a graph of two quantities that he measured and said, “The points all lie on a line except one, which is a little bit above the line. This means that the quantities can’t be proportional.” Do you agree with Diego? Explain.
   
4. The graph shows that while it was being filled, the amount of water in gallons in a swimming pool was approximately proportional to the time that has passed in minutes.
   a. About how much water was in the pool after 25 minutes?
   b. Approximately when were there 500 gallons of water in the pool?
   c. Estimate the constant of proportionality for the number of gallons of water per minute going into the pool.
   

The Open Up Resources math curriculum is free to download from the Open Up Resources website and is also available from Illustrative Mathematics.

Try the free Mathway calculator and problem solver below to practice various math topics. Try the given examples, or type in your own problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.