Probability and Statistics

Example:
40 students were given a test. The table below shows the cumulative frequency of the results obtained.

Mark	10	20	30	40	50	60	70	80	90	100
Number of students scoring the mark or less	2	5	8	11	18	24	30	32	37	40

a) State the probability that a student chosen at random will have a mark less than or equal to 60.

b) Two students are chosen at random from the 40 students. Find the probability that neither have marks more than 60.

c) A second group of students were tested and one-fifth of them scored more than 70 marks. If a student is now chosen at random from each group, find the probability that at least one student would have scored more than 70.

Solution:
a) From the table, we see that there were 24 students who scored 60 marks or less. Therefore, the probability of selecting a student with 60 marks or less

b) Neither have marks more than 60 means that both have marks less than or equal to 60.

Probability =
 

c) From the table, we can work out that there are 40 – 30 = 10 students with greater than 70 marks. Therefore, the probability of selecting a student in the first with greater than 70 marks

 

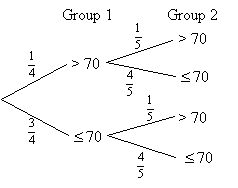
Probability that at least one student would have scored more than 70 is

 

Introduction to Probability and Statistics
Introduce the basic definitions and nomenclature of probability and statistics.

Definition of Sets and Elements

• Show Video

Definition of Sample Spaces & Factorials

• Show Video

Definition of Event

• Show Video

Link to the Probability & Statistics Playlist

Check out our most popular games!
Fraction Concoction	Fact Family Game	Number Bond Garden
Online Addition Subtraction Game	Penguin Solitaire	Sawayama Solitaire
Ark Solitaire	Eldritch Invasion	Shenzhen Solitaire

Check out more Solitaire games here.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.