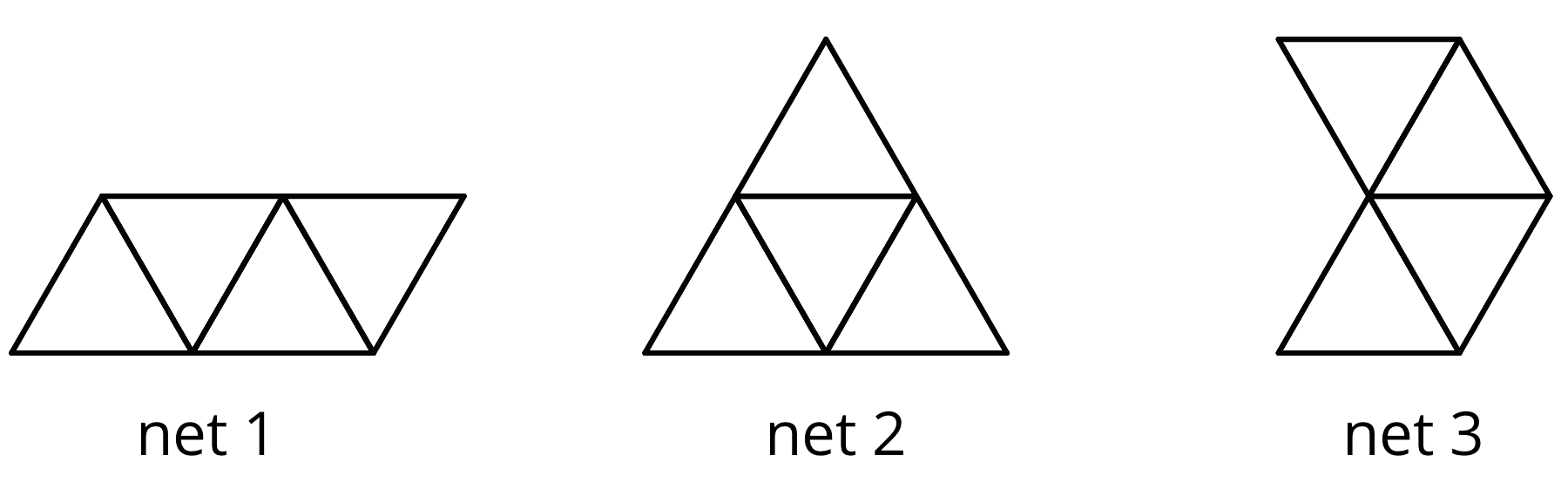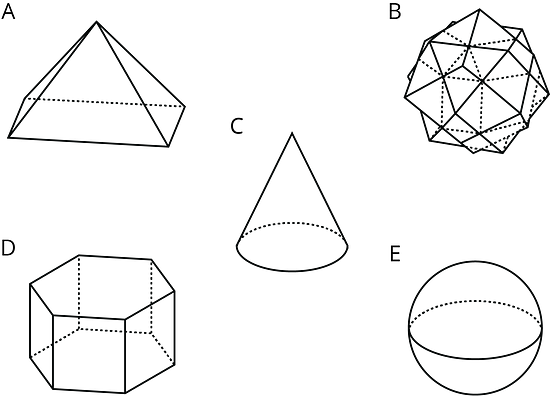Illustrative Mathematics Unit 6.1, Lesson 13: Polyhedra

Related Pages
Illustrative Math
Grade 6
Math Worksheets

**Polyhedra**
Let’s investigate polyhedra.

Illustrative Math Unit 6.1, Lesson 13 (printable worksheets)

13.1 - What are Polyhedra?

Here are pictures that represent polyhedra:

Here are pictures that do not represent polyhedra:

1. Your teacher will give you some figures or objects. Sort them into polyhedra and non-polyhedra.

2. What features helped you distinguish the polyhedra from the other figures?

• Features of Polyhedra

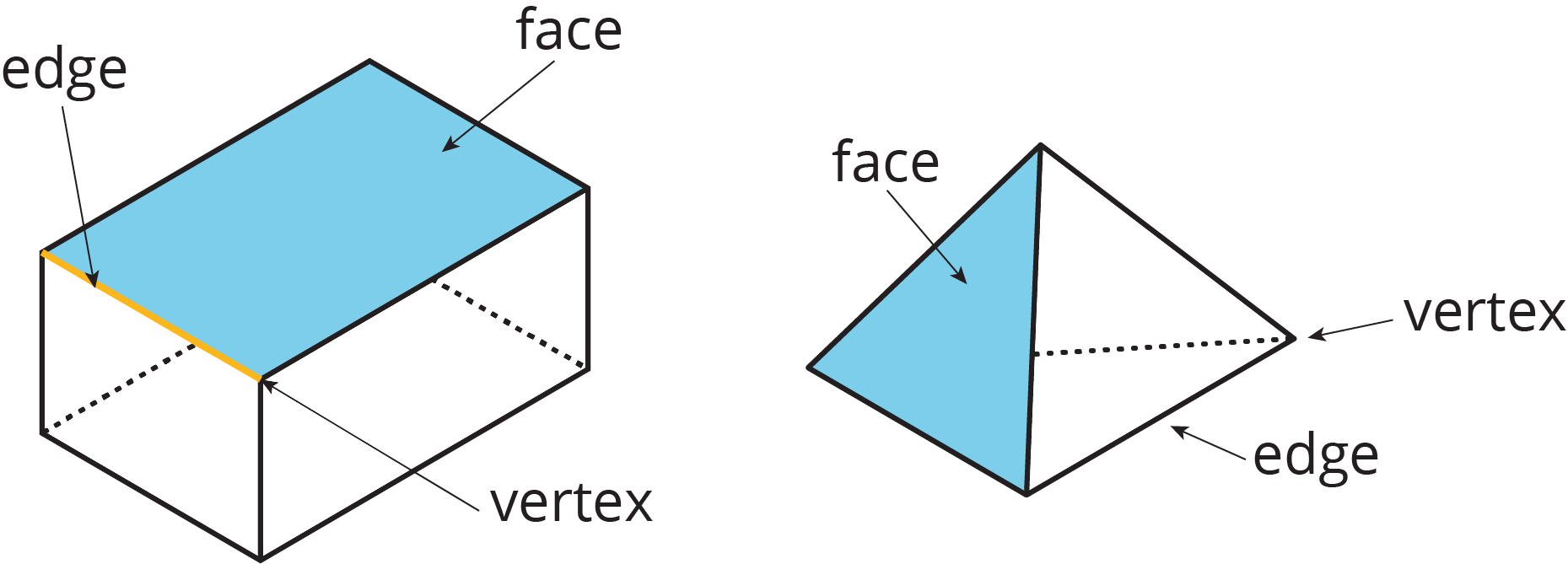
  A polyhedron (plural polyhedra) is a three-dimensional figure built from filled-in polygons. The polygons are called faces. The places where the sides of the faces meet are called edges. The “corners” are called vertices (singular vertex).

  

  All edges of polygons meet another polygon along a complete edge.

  Each polygon meets one and only one polygon on each of the edges.

  The polygons enclose a three-dimensional region.

• See Video 1 for Whole Lesson
• See Video 2 for Whole Lesson

13.2 - Prisms and Pyramids

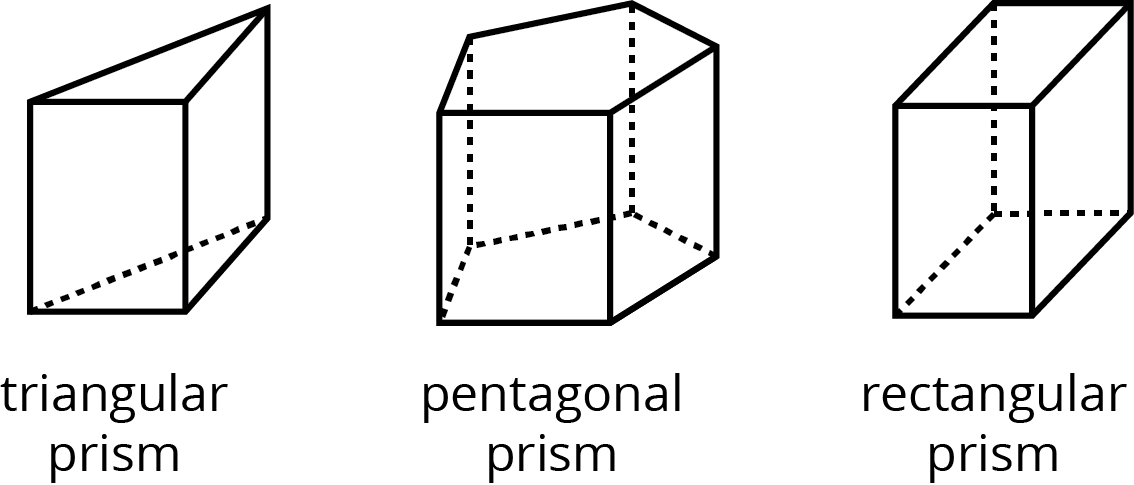
1. Here are some polyhedra called prisms.

• Show Image
  

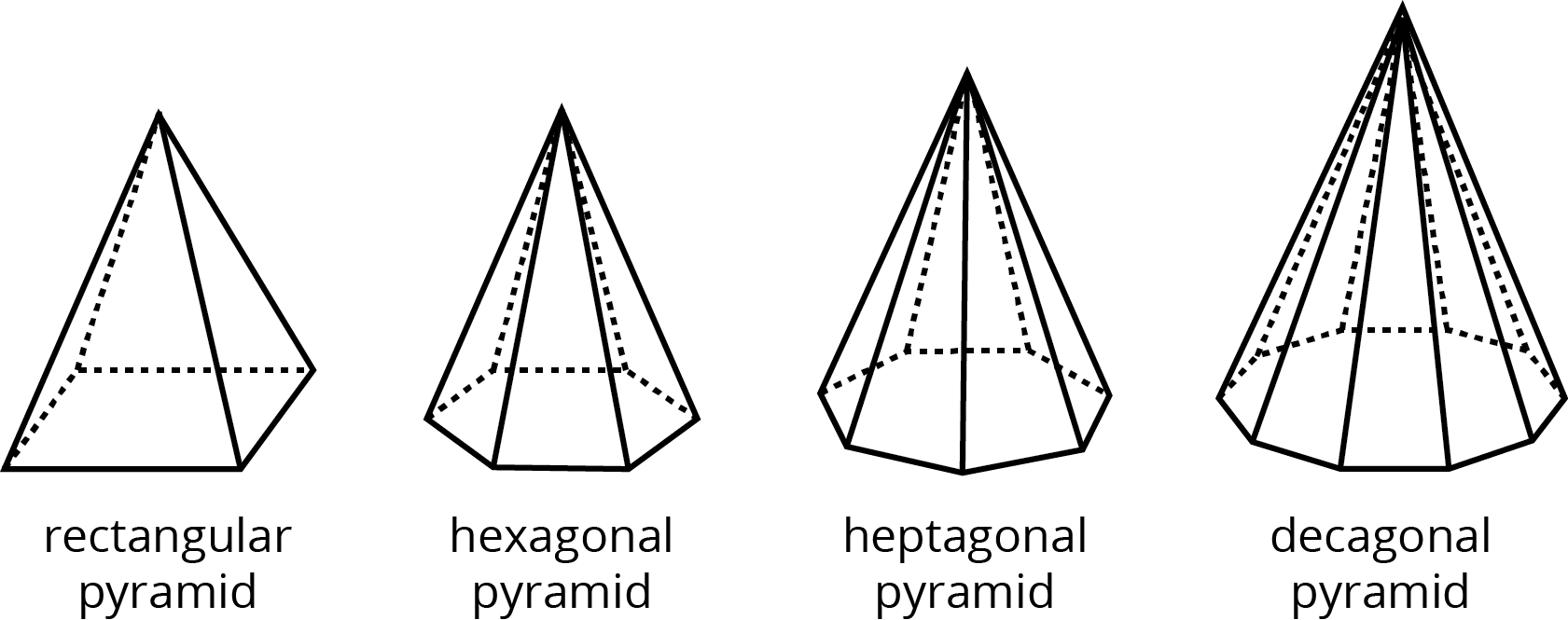
Here are some polyhedra called pyramids.

• Show Image
  

a. Look at the prisms. What are their characteristics or features?
b. Look at the pyramids. What are their characteristics or features?

2. A net is a two-dimensional representation of a polyhedron. It is composed of polygons that form the faces of a polyhedron. A net can be folded to make a polyhedron. You may explore net folding with these applets (optional).
   Which of the following nets can be folded into Pyramid P? Select all that apply.

• Show Image
  

3. Your teacher will give your group a set of polygons and assign a polyhedron.

a. Decide which polygons are needed to compose your assigned polyhedron. List the polygons and how many of each are needed.
b. Arrange the cut-outs into a net that, if taped and folded, can be assembled into the polyhedron. Sketch the net. If possible, find more than one way to arrange the polygons (show a different net for the same polyhedron).

• Show Answers

  1. a. A prism has two parallel, identical faces called bases and a set of rectangles connecting the bases. Prisms are named for the shape of the bases. For example, if the base of a prism is a pentagon, then the prism is called a “pentagonal prism”.
     b. A pyramid has one face called the base that can be any polygon, and a set of faces that are all triangles. Each edge of the base is shared with an edge of a triangle. All of these triangles meet at a single vertex. Pyramids are named for the shape of their base. For example, if the base of a pyramid is a square, then the pyramid is called a “square pyramid”.

  2. Net 1 and Net 2 can be folded into Pyramid P. Net 3 cannot; two of the triangles will overlap.

  3. To compose a prism, you need the right polygons for its two bases, and one rectangle for every side of one base.
     To compose a pyramid, you need the right polygon for its base, and one triangle for every side of the base.

What is the smallest number of faces a polyhedron can possibly have? Explain how you know.

• Show Answer

  The polyhedron with the smallest number of faces will be made from polygons with the smallest number of sides. The smallest number of sides a polygon can have is 3, a triangle.
  In a polyhedron made from triangles, each edge of any one triangular face must meet another triangular face. Since each face has 3 edges, the total number of faces must be 1 + 3 = 4.
  The smallest number of faces a polyhedron can have is 4.

13.3 - Assembling Polyhedra

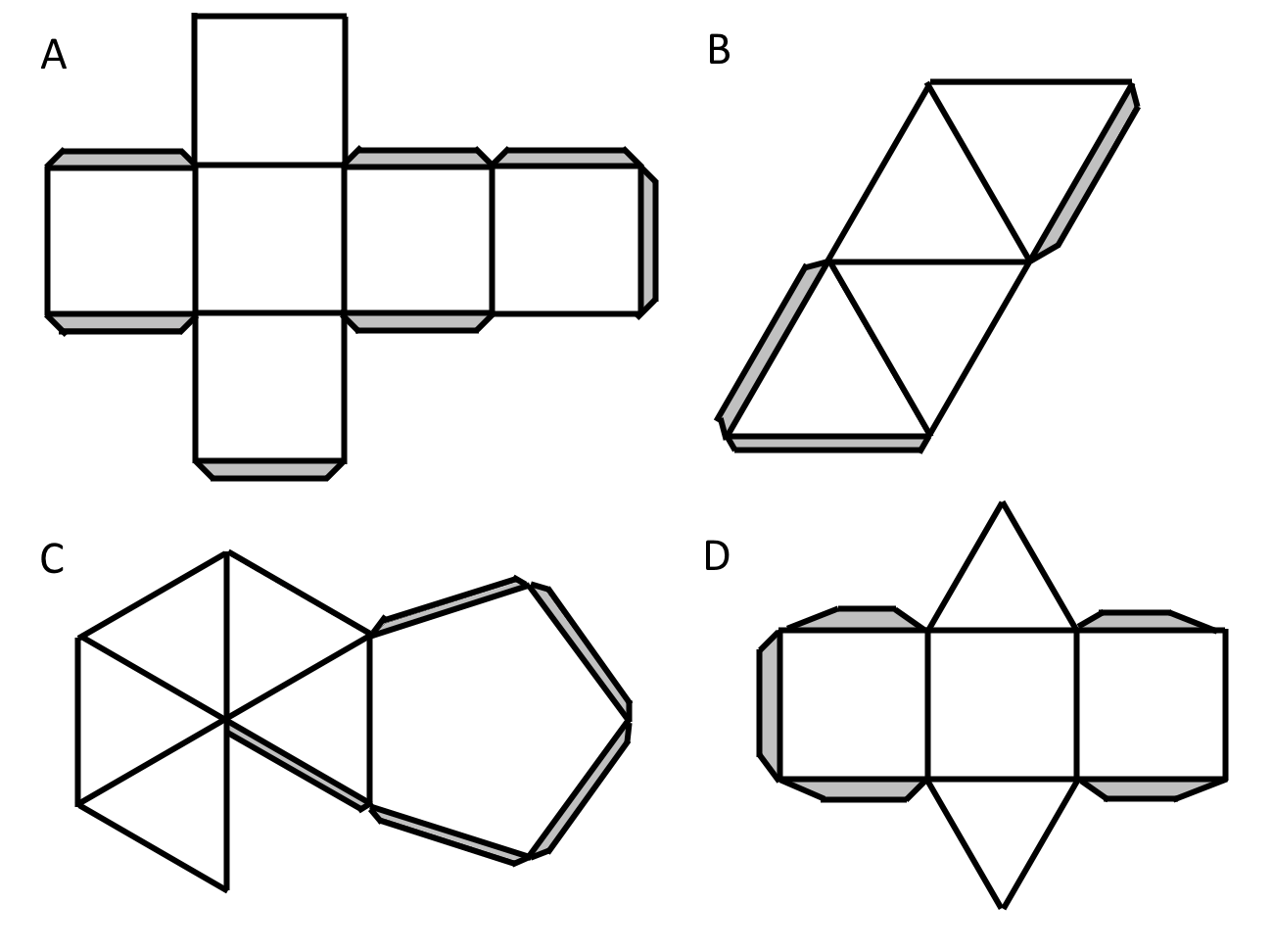
1. Your teacher will give you the net of a polyhedron. Alternatively, you may print out the following nets. Cut out the net, and fold it along the edges to assemble a polyhedron. Tape or glue the shaded flaps so that there are no unjoined edges.

• Show Image

  
  

  (Source: polyhedra.net/gijs)

2. How many vertices, edges, and faces are in your polyhedron?

• Show Answers
  1. Net A folds into a cube. Net B folds into a tetrahedron (a triangular pyramid). Net C folds into a pentagonal pyramid. Net D folds into a triangular prism.
     

  
  

  (Photos from polyhedra.net/gijs)

2. A: 8 vertices, 12 edges, 6 faces
   B: 4 vertices, 6 edges, 4 faces
   C: 6 vertices, 10 edges, 6 faces
   D: 6 vertices, 9 edges, 5 faces

Lesson 13 Summary

A polyhedron is a three-dimensional figure composed of faces. Each face is a filled-in polygon and meets only one other face along a complete edge. The ends of the edges meet at points that are called vertices.

• Show Image
  

A polyhedron always encloses a three-dimensional region.

The plural of polyhedron is polyhedra. Here are some drawings of polyhedra:

• Show Image
  

A prism is a type of polyhedron with two identical faces that are parallel to each other and that are called bases. The bases are connected by a set of rectangles (or sometimes parallelograms).

A prism is named for the shape of its bases. For example, if the base is a pentagon, then it is called a “pentagonal prism”.

• Show Image
  

A pyramid is a type of polyhedron that has one special face called the base. All of the other faces are triangles that all meet at a single vertex.

A pyramid is named for the shape of its base. For example, if the base is a pentagon, then it is called a “pentagonal pyramid”.

• Show Image
  

A net is a two-dimensional representation of a polyhedron. It is composed of polygons that form the faces of a polyhedron.

• Show Image
  

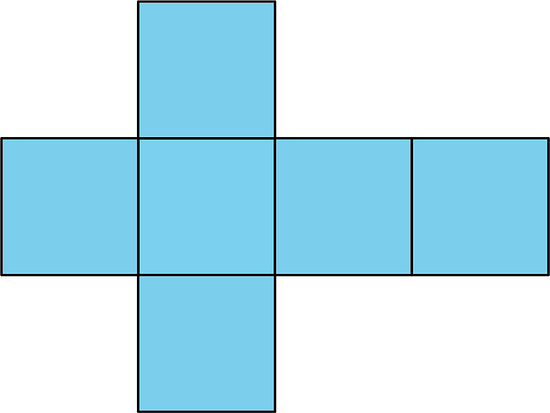
A cube has 6 square faces, so its net is composed of six squares, as shown here.

A net can be cut out and folded to make a model of the polyhedron.

In a cube, every face shares its edges with 4 other squares. In a net of a cube, not all edges of the squares are joined with another edge. When the net is folded, however, each of these open edges will join another edge.

It takes practice to visualize the final polyhedron by just looking at a net.

Glossary Terms

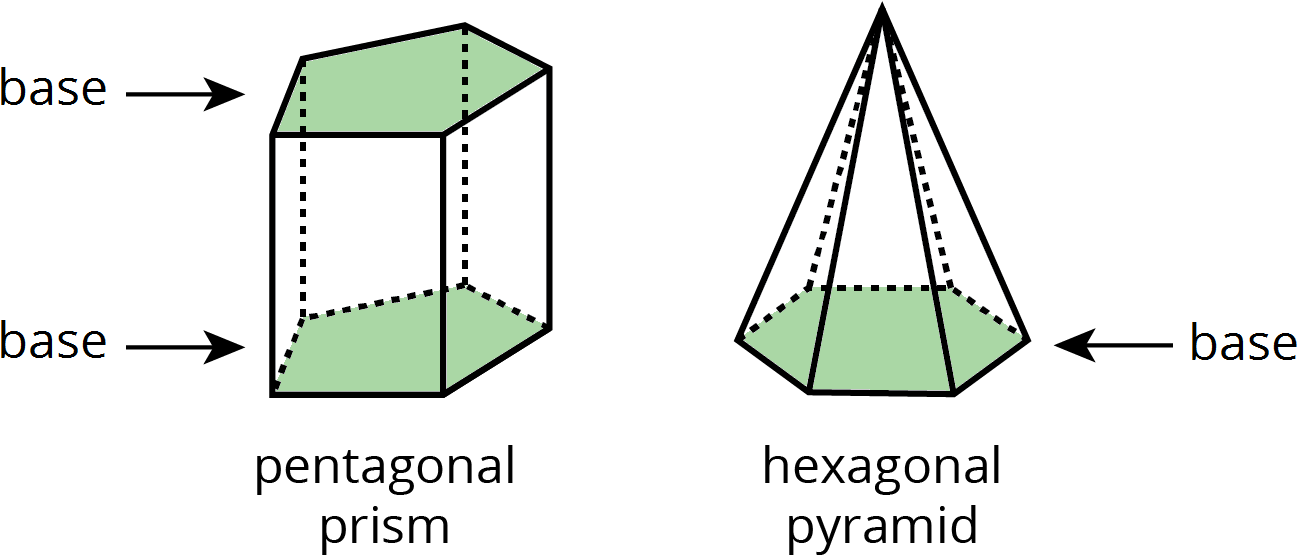
base (of a prism or pyramid)

The word base can also refer to a face of a polyhedron.

A prism has two identical bases that are parallel. A pyramid has one base.

A prism or pyramid is named for the shape of its base.

• Show Image
  

---

face

Each flat side of a polyhedron is called a face. For example, a cube has 6 faces, and they are all squares.

---

net

A net is a two-dimensional figure that can be folded to make a polyhedron.

Here is a net for a cube.

• Show Image
  

polyhedron

A polyhedron is a closed, three-dimensional shape with flat sides. When we have more than one polyhedron, we call them polyhedra.

Here are some drawings of polyhedra.

• Show Image
  

prism

A prism is a type of polyhedron that has two bases that are identical copies of each other. The bases are connected by rectangles or parallelograms.

Here are some drawings of prisms.

• Show Image
  

pyramid

A pyramid is a type of polyhedron that has one base. All the other faces are triangles, and they all meet at a single vertex.

Here are some drawings of pyramids.

• Show Image
  

Practice Problems

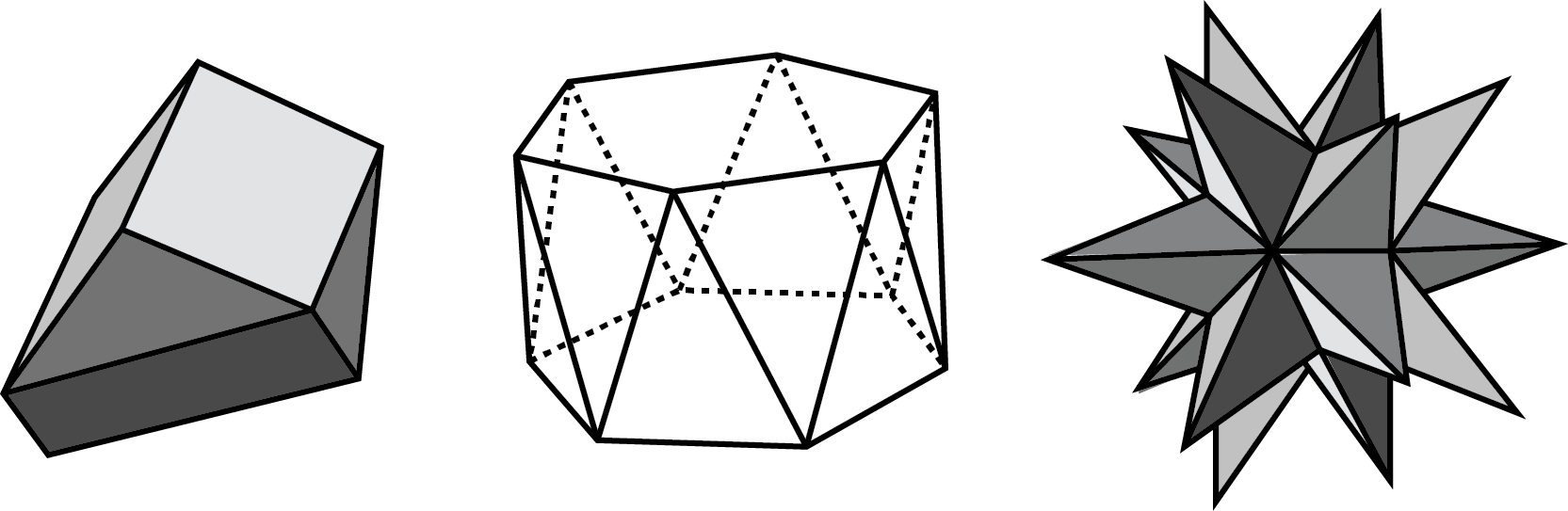
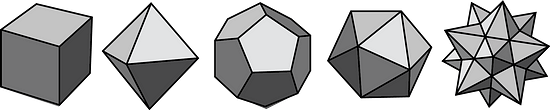
1. Select all the polyhedra.

• Show Image
  
• Show Answer

  A, B, and D are polyhedra.
  C and E are not polygons because they are not made of polygonal faces.

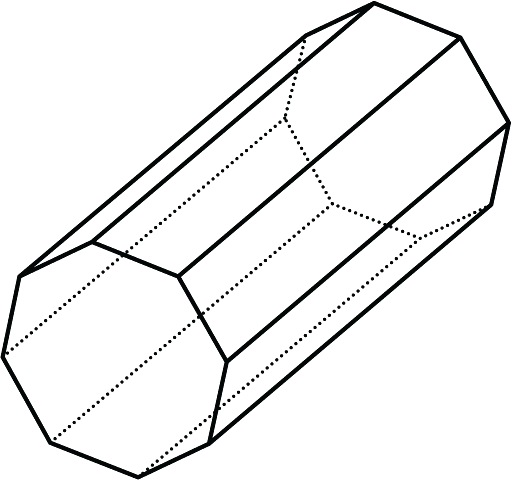
2. a. Is this polyhedron a prism, a pyramid, or neither? Explain how you know.
b. How many faces, edges, and vertices does it have?

• Show Image
  
• Show Answers

  a. This polyhedron is a prism. It has two identical, parallel octagonal bases joined by rectangular faces.
  b. This prism has 10 faces, 24 edges, and 16 vertices.

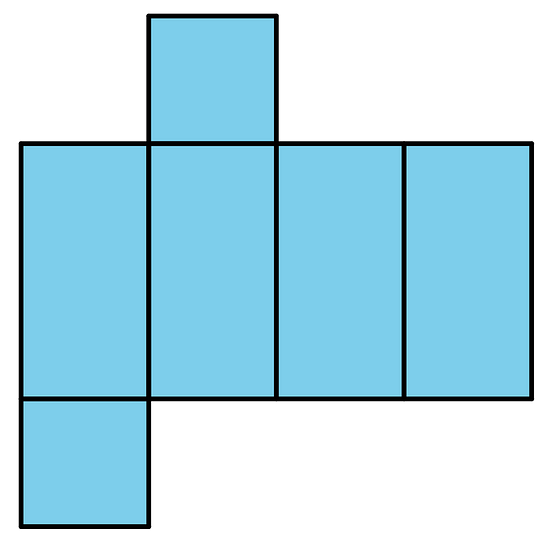
3. Tyler said this net cannot be a net for a square prism because not all the faces are squares.

• Show Image
  

Do you agree with Tyler? Explain your reasoning.

• Show Answer

  Tyler is incorrect. Prisms are named after the shape of their bases. This net has two identical squares which can form the base of a square prism.

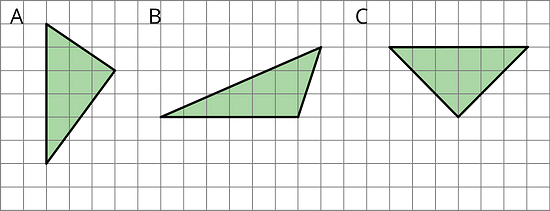
4. Explain why each of these triangles has an area of 9 square units.

• Show Image
  
• Show Answer

  All the triangles have a base of 6 units and a height of 3 units.
  A = ½ · b · h
  A = ½ × 6 units × 3 units
  A = 9 square units

5. a. A parallelogram has a base of 12 meters and a height of 1.5 meters. What is its area?
b. A triangle has a base of 16 inches and a height of ⅛ inches. What is its area?
c. A parallelogram has an area of 28 square feet and a height of 4 feet. What is its base?
d. A triangle has an area of 32 square millimeters and a base of 8 millimeters. What is its height?

• Show Answers

  a. Area of parallelogram = b · h
  12 meters × 1.5 meters = 18 square meters

  b. Area of triangle = ½ · b · h
  ½ × 16 inches × ⅛ inches = 2 square inches

  c. Area of parallelogram = b · h
  28 square feet = b × 4 feet
  b = 28 square feet ÷ 4 feet = 7 feet

  d. Area of triangle = ½ · b · h
  32 square millimeters = ½ × 8 millimeters × h
  h = 32 square millimeters ÷ 8 millimeters = 4 millimeters

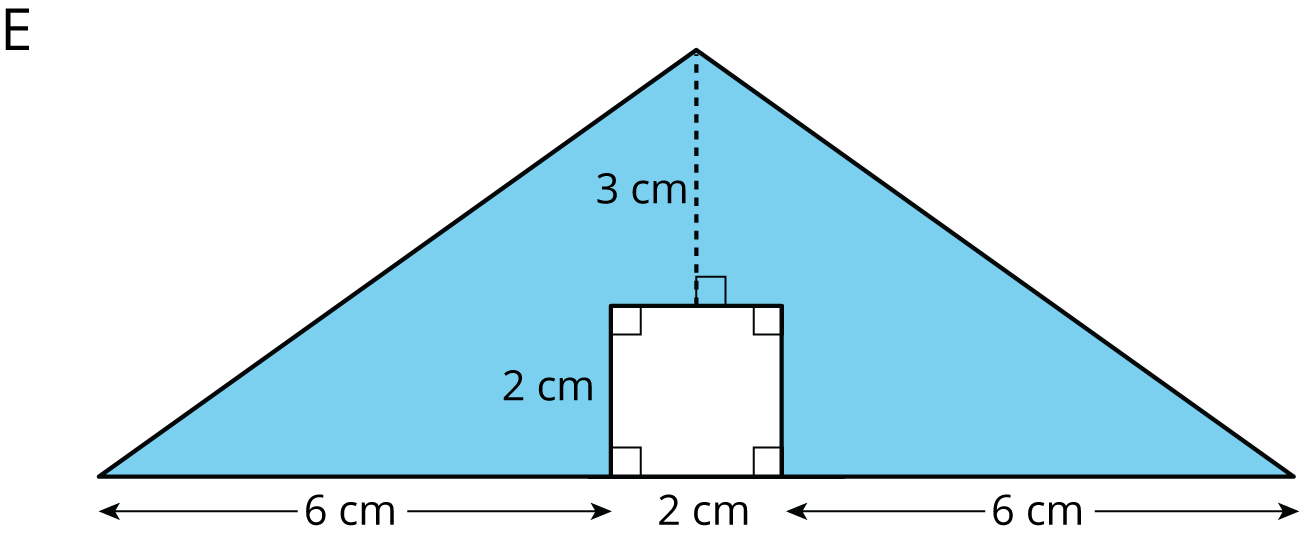
6. Find the area of the shaded region. Show or explain your reasoning.

• Show Image
  
• Show Answer

  The base of the triangle encompassing the whole figure is 6 cm + 2 cm + 6 cm = 14 cm.
  The height of the triangle is 3 cm + 2 cm = 5 cm.
  The area of this triangle is ½ × 14 cm × 5 cm = 35 square cm.

  The area of the unshaded square is 2 cm × 2 cm = 4 square cm.

  The area of the shaded region is 35 square cm - 4 square cm = 31 square cm.

Try the free Mathway calculator and problem solver below to practice various math topics. Try the given examples, or type in your own problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.