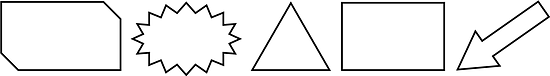OML Search

Illustrative Mathematics Unit 6.1, Lesson 11: Polygons

Related Topics:
Math Worksheets




Learn about how to describe the characteristics of a polygon using mathematical vocabulary, and to reason about the area of polygons. After trying the questions, click on the buttons to view answers and explanations in text or video.

Return to the list of Illustrative Math lessons


Polygons
Let’s investigate polygons and their areas.

Illustrative Math Unit 6.1, Lesson 11 (printable worksheets)

11.1 - Which One Doesn’t Belong: Bases and Heights

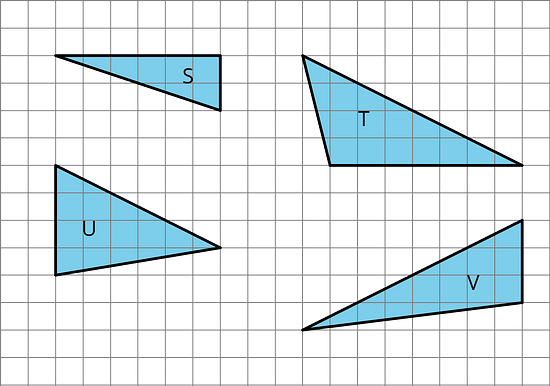
Which one doesn't belong? Give reasons. Focus on describing the characteristics of the triangle you choose.

Four triangles on a grid, labeled S, T, U, and V.

  • See Possible Answers

    All of the triangles are different from every other triangle in some way. For example:

    • Triangle S is the only one with a right angle.
    • Triangle T is the only one that does not have a vertical side.
    • Triangle U is the only one with three acute angles.
    • Triangle V has the longest sides.

    These are examples; any one of these triangles might not belong, for other reasons you might think of.

  • See Video 1 for Whole Lesson
  • See Video 2 for Whole Lesson




11.2 - What Are Polygons?

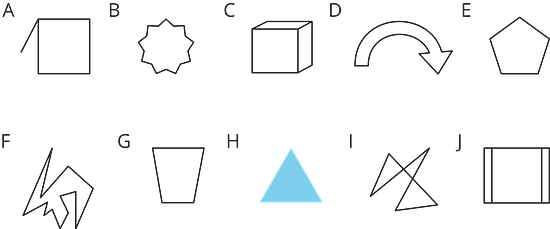
Here are five polygons:

Here are six figures that are not polygons:

1. Circle the figures that are polygons.

2. What do the figures you circled have in common? What characteristics helped you decide whether a figure was a polygon?

  • Answers and Definition of a Polygon

    1. The polygons are B, D, E, F, G, and H.

    2. The characteristics of a polygon are:

    • It is composed of line segments. Line segments are always straight.
    • Each line segment meets one and only one other line segment at each end.
    • The line segments never cross each other except at the end points.
    • It is two-dimensional.

    The line segments in a polygon are called the edges or sides. A point where edges meet is called a vertex (plural vertices).

    Polygons always enclose a region. "Finding the area of a polygon" is shorthand for "finding the area of the region a polygon encloses."


11.3 - Quadrilateral Strategies

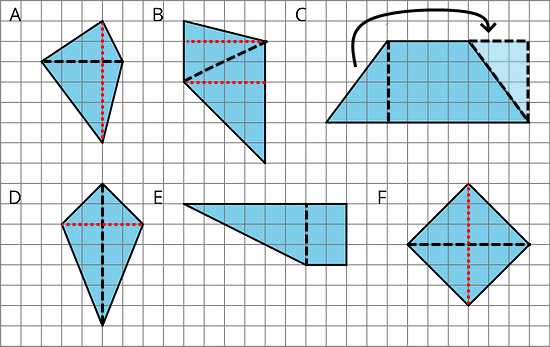
Find the area of two quadrilaterals of your choice. Show your reasoning.

  • Hints

    Use any strategies from the previous lessons, such as decomposing or enclosing the quadrilateral, to calculate the area.

  • See Possible Answers

    Six quadrilaterals labeled A--F, which have been decomposed, rearranged, or enclosed in other polygons with dashed lines to help find the area of the original quadrilaterals.

    A can be divided into 2 triangles along the black dashed lines. Red dotted lines indicate the height of each triangle. The area of A is (½ × 4 units × 2 units) + (½ × 4 units × 4 units) = 12 square units.

    B can be divided into 2 triangles. The area of B is (½ × 4 units × 2 units) + (½ × 4 units × 4 units) = 12 square units.

    C can be decomposed and rearranged to make a rectangle. The area of C is 7 units × 4 units = 28 square units.

    D can de divided into 2 identical triangles. The area of D is 2 × (½ × 7 units × 2 units) = 14 square units.

    E can be divided into a right triangle and a rectangle. The area of E is (½ × 6 units × 3 units) + (2 units × 3 units) = 14 square units.

    F can be divided into 2 identical triangles. The area of F is 2 × (½ × 6 units × 3 units) = 18 square units.


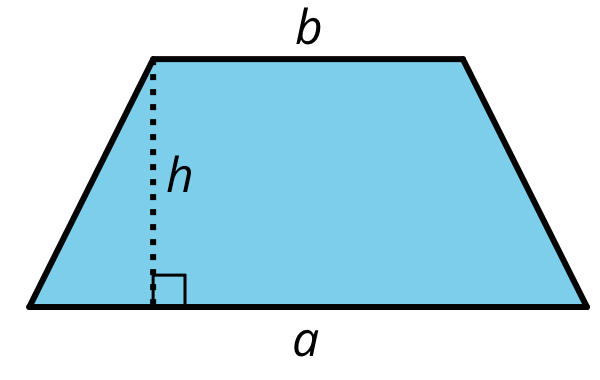
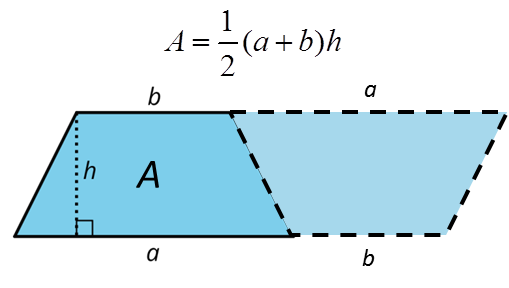
Here is a trapezoid. a and b represent the lengths of its bottom and top sides. The segment labeled h represents its height; it is perpendicular to both the top and bottom sides.

Apply area-reasoning strategies—decomposing, rearranging, duplicating, etc.—on the trapezoid so that you have one or more shapes with areas that you already know how to find.

Use the shapes to help you write a formula for the area of a trapezoid. Show your reasoning.

  • Hints

    If you decompose the trapezoid, how would you know what the lengths of the decomposed segments of a or b are? Is there another way to approach this?

    Try to create a parallelogram.

  • See Possible Answers

    A parallelogram composed of two identical trapezoids, with base a+b and height h, demonstrating how a trapezoid can be duplicated to make a parallelogram.

    A trapezoid with parallel sides a and b and height h can be duplicated and inverted to create a parallelogram with base a+b and height h.
    The area of this new parallelogram is (a + b) · h.
    The original trapezoid is half of the parallelogram, so its area A = ½ · (a + b) · h. This is the formula for the area of a trapezoid.




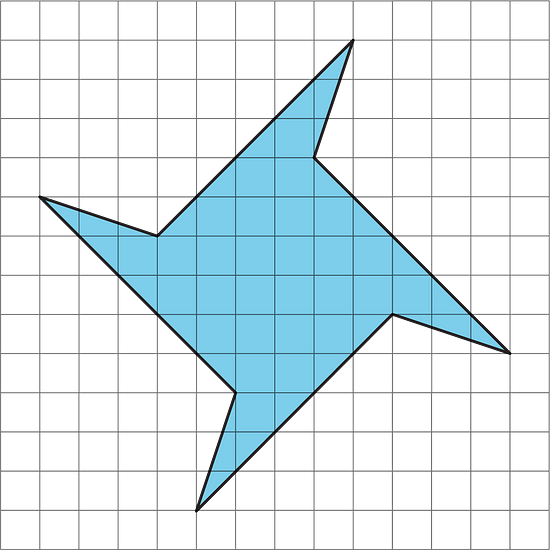
11.4 - Pinwheel

Find the area of the shaded region in square units. Show your reasoning.

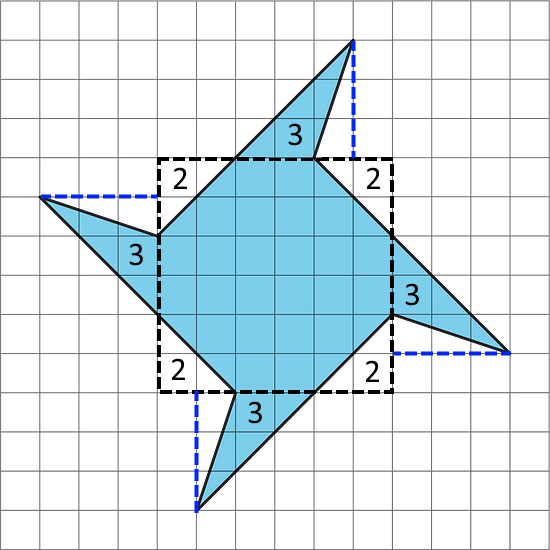
  • See Possible Answers

    A shaded pinwheel-shaped polygon on a grid. The central region of the pinwheel has been enclosed in a square.

    The figure can be decomposed into an octagon and four shaded triangles.
    The area of the four triangles is 4 × ½ × 2 units × 3 units = 12 square units.
    The octagon can be enclosed in a square with area 6 units × 6 units = 36 units.
    The area of the four unshaded triangles is 4 × ½ × 2 units × 2 units = 8 square units.
    Hence, the area of the octagon is 36 units - 8 units = 28 square units.
    The total area of the shaded region is 12 square units + 28 square units = 40 square units.


Lesson 11 Summary

A polygon is a two-dimensional figure composed of straight line segments.

Each end of a line segment connects to one other line segment. The point where two segments connect is a vertex. The plural of vertex is vertices.

The segments are called the edges or sides of the polygon. The sides never cross each other. There are always an equal number of vertices and sides.

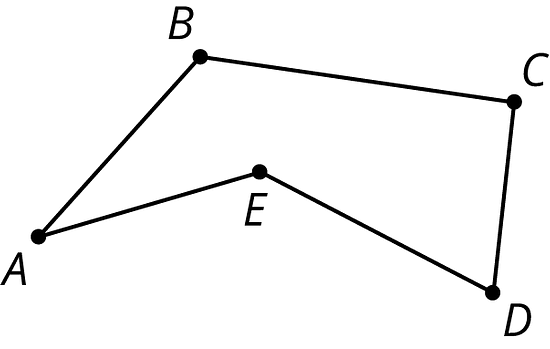
Here is a polygon with 5 sides. The vertices are labeled A, B, C, D, and E.

A polygon encloses a region. To find the area of a polygon is to find the area of the region inside it.

We can find the area of a polygon by decomposing the region inside it into triangles and rectangles.

The first two diagrams show the polygon decomposed into triangles and rectangles; the sum of their areas is the area of the polygon. The last diagram shows the polygon enclosed in a rectangle; subtracting the areas of the triangles from the area of the rectangle gives us the area of the polygon.

Glossary Terms

edge

Each straight side of a polygon is called an edge.

For example, the edges of this polygon are segments AB, BC, CD, DE, and EA.

polygon

A polygon is a closed, two-dimensional shape with straight sides that do not cross each other.

Figure ABCDE is an example of a polygon.

quadrilateral

A quadrilateral is a type of polygon that has 4 sides. A rectangle is an example of a quadrilateral. A pentagon is not a quadrilateral, because it has 5 sides.

vertex

A vertex is a point where two or more edges meet. When we have more than one vertex, we call them vertices.

The vertices in this polygon are labeled A, B, C, D, and E.


Practice Problems

1. Select all the polygons.

  • Answers

    A, B, C, and E are polygons.
    D is not a polygon because it has line segments with ends that do not meet other line segments; it does not enclose an area.
    F is not a polygon because it has line segments which meet multiple other line segments at their ends (because it is a representation of a three-dimensional shape).


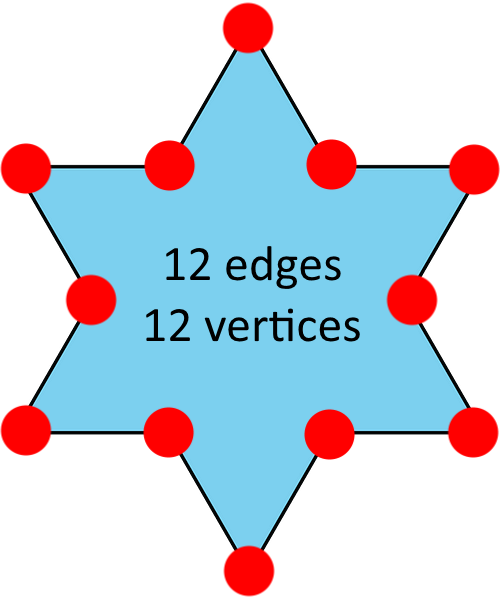
2. Mark each vertex with a large dot. How many edges and vertices does this polygon have?

  • Answers

    Solid blue six pointed star. The twelve vertices have been marked with large red dots.

    This polygon has 12 edges and 12 vertices.


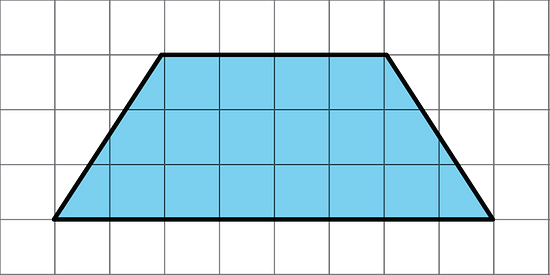
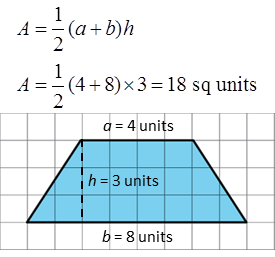
3. Find the area of this trapezoid. Explain or show your strategy.

  • Hints

    Earlier in this lesson you were asked to find the area of a trapezoid and determine a formula for finding the area of a trapezoid. You may revise that strategy, use the formula, or use another strategy.

  • See Possible Answers

    Trapezoid on a grid. Short side 4, long side 8, height 3, area 18 square units.

    Earlier in this lesson, we found that the formula for the area of a trapezoid is A = ½ · (a + b) · h, where a and b are the trapezoid's parallel sides.
    Hence, the area of this trapezoid is ½ × (4 units + 8 units) × 3 units = 18 square units.


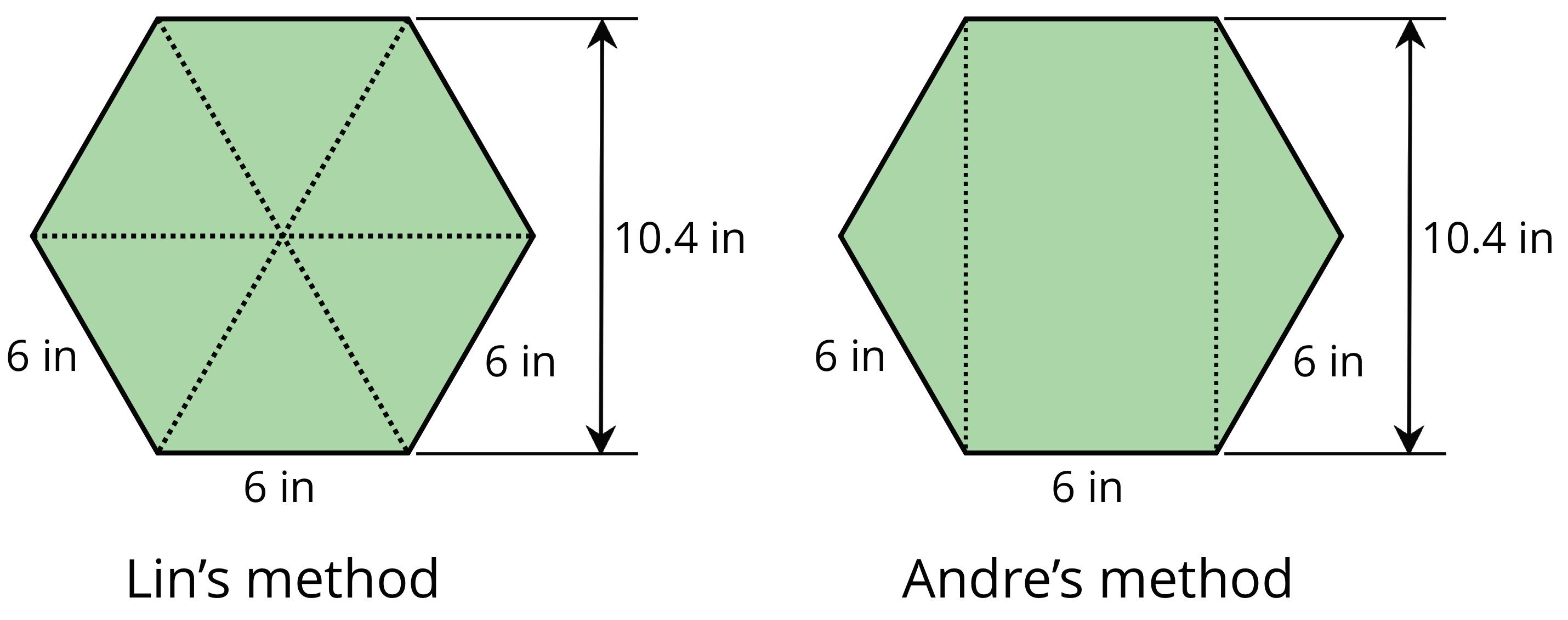
4. Lin and Andre used different methods to find the area of a regular hexagon with 6-inch sides. Lin decomposed the hexagon into six identical triangles. Andre decomposed the hexagon into a rectangle and two triangles.

Find the area of the hexagon using each person’s method. Show your reasoning.

  • Hints

    Notice that in both methods, you will have to deduce the heights of the triangles from the information given.

  • Answers

    Two identical hexagons labeled “Lin’s method” and “Andre’s method”. Each hexagon has three sides labeled 6 inches and an arrow indicating total height labeled 10.4 inches. “Lin’s method” is divided into six equal triangles, and Andre’s method is decomposed into a rectangle made of lines extending from one side to the opposite side, with a triangle on either side of the rectangle. The heights of the triangles have been labeled.

    Both methods, if done correctly, will give the same answer.

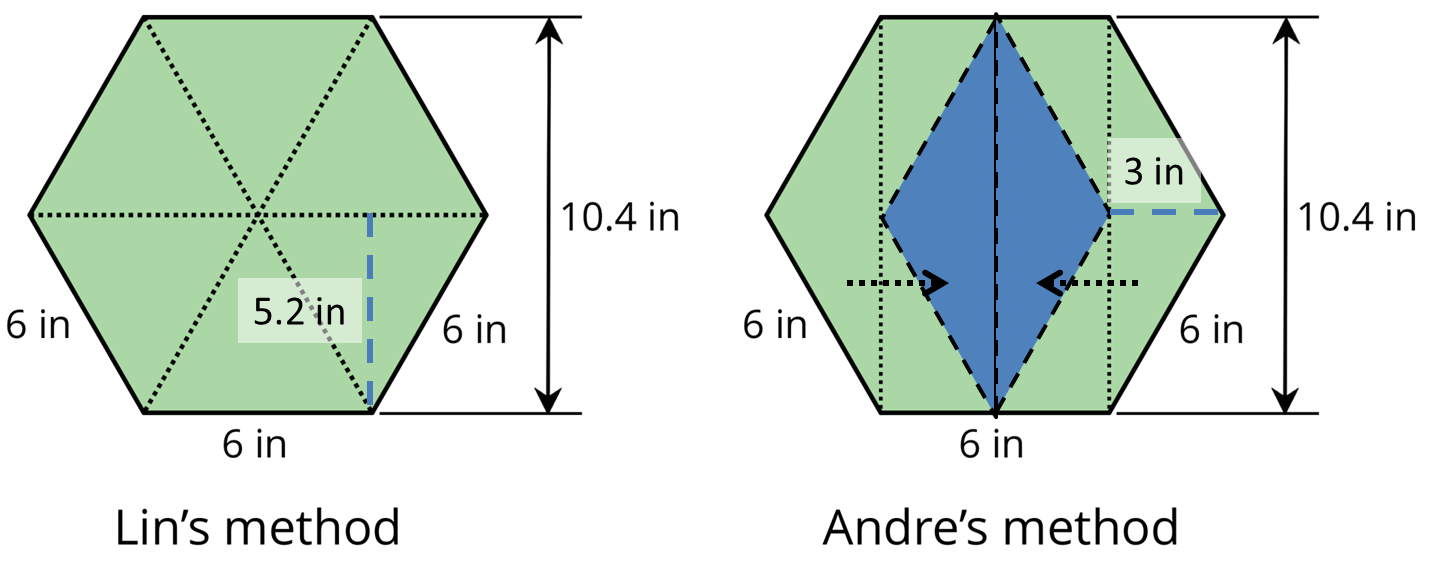
    Lin's method: The six triangles are equilateral, so all three sides of any one triangle measure 6 in.
    Hence, the height of any one triangle, as shown by the blue dashed line, is 10.4 in ÷ 2 = 5.2 in.
    The area of one triangle is ½ × 6 in × 5.2 in = 15.6 sq in.
    The area of all six triangles, and hence the area of the hexagon, is 6 × 15.6 sq in = 93.6 sq in.

    Andre's method: Note how the two side triangles fit into the middle rectangle. This is a property of a regular hexagon. The height of the triangles is therefore 6 in ÷ 2 = 3 in.
    The area of both triangles is 2 × ½ × 10.4 in × 3 in = 31.2 sq in.
    The area of the rectangle is 6 in × 10.4 in = 62.4 in.
    The area of the hexagon is 31.2 sq in + 62.4 sq in = 93.6 sq in.


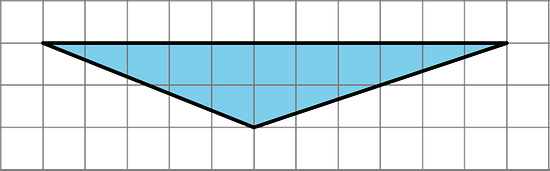
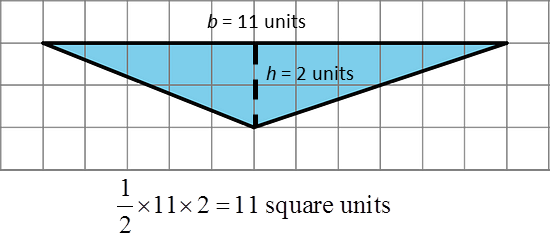
5. Identify a base b and a corresponding height h that can be used to find the area of this triangle. Label the base b and the corresponding height h.
Find the area of the triangle. Show your reasoning.

  • Answers

    A triangle that has two vertices 11 units apart from one another horizontally, and a third vertex that is 2 units below the horizontal line and five units right of the left vertex and 6 units right of the left vertex. A height that is 2 units has been drawn connecting the horizontal line to the vertex below it. The horizontal line is labeled b and the height is labeled h.

    The area of this triangle is ½ × 11 units × 2 units = 11 square units.


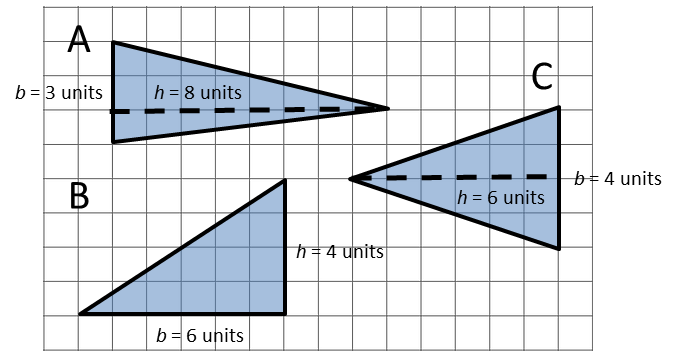
6. On the grid, draw three different triangles with an area of 12 square units. Label the base and height of each triangle.

  • See Possible Answers

    Three triangles drawn on a grid that is 16 units by 10 units. Triangle A has a base of 3 units and a height of 8 units. Triangle B has a base of 6 units and a height of 4 units. Triangle C has a base of 4 units and a height of 6 units.

    A: ½ × 3 units × 8 units = 12 sq units
    B: ½ × 6 units × 4 units = 12 sq units
    C: ½ × 4 units × 6 units = 12 sq units




The Open Up Resources math curriculum is free to download from the Open Up Resources website and is also available from Illustrative Mathematics.

Try the free Mathway calculator and problem solver below to practice various math topics. Try the given examples, or type in your own problem and check your answer with the step-by-step explanations.
Mathway Calculator Widget


OML Search


We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.



 
Back to Top | Interactive Zone | Home

Copyright © 2005, 2024 - OnlineMathLearning.com.
Embedded content, if any, are copyrights of their respective owners.