Polygons

Related Topics:
More Lessons for GRE Math

Math Worksheets

These lessons are part of a series on the quantitative reasoning section of the GRE revised General Test. In this lesson, we will learn:

• polygons
• interior and exterior angles of regular polygons

Polygons

A polygon is a closed figure formed by three or more line segments, called sides. Each side is joined to two other sides at its endpoints, and the endpoints are called vertices.

In this discussion, the term “polygon” means “convex polygon,” that is, a polygon in which the measure of each interior angle is less than 180°. The figures below are examples of such polygons.

Angles of a Polygon

The simplest polygon is a triangle. We know that the sum of interior angles in a triangle is 180º.

A quadrilateral can be divided into 2 triangles, a pentagon can be divided into 3 triangles, and a hexagon can be divided into 4 triangles as shown below.

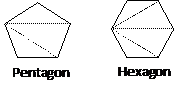
If a polygon has n sides, it can be divided into n − 2 triangles. Since the sum of the measures of the interior angles of a triangle is 180º it follows that the sum of the measures of the interior angles of an n-sided polygon is (n − 2)(180º)

For example, the sum for a quadrilateral (n = 4) is
(4 − 2)(180º) = 360º
and the sum for a hexagon (n = 6) is
(6 − 2)(180º) = 720º

A polygon in which all sides are congruent and all interior angles are congruent is called a regular polygon. For example, in a regular octagon (8 sides), the sum of the measures of the interior angles is (8 − 2)(180º) = 1080º
Therefore, the measure of each angle is 1080º ÷ 8 = 135º

The perimeter of a polygon is the sum of the lengths of its sides. The area of a polygon refers to the area of the region enclosed by the polygon

This video shows the formula for the interior and exterior angles of a polygon. The following video shows how to determine the sum of the interior and exterior angles of a polygon.