Construct A Perpendicular Bisector
In these lessons, we will learn how to construct the perpendicular bisector of a line segment using a compass and a straightedge or ruler. We will also learn how a perpendicular bisector can be used to form a rhombus or kite and to find the midpoint of a line segment.
Related Pages
More Geometric Constructions & Geometry Lessons
The following diagram shows the perpendicular bisector of the line segment AB. Scroll down the page for examples and step-by-step solutions on how to construct a perpendicular bisector.
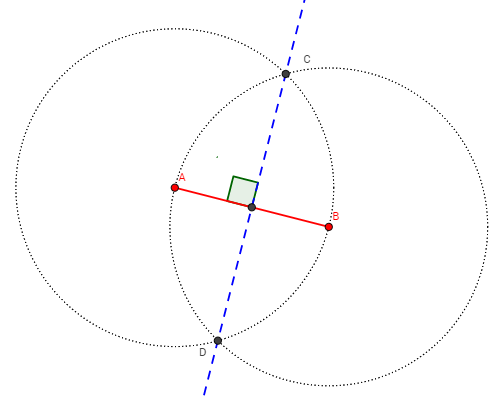
The perpendicular bisector of a line segment AB is a line that divides the line AB into two equal parts at a right angle.
How to construct a perpendicular bisector?
Example:
Construct a perpendicular bisector of the given line segment AB.
Solution:
Step 1: Stretch your compasses until it is more then half the length of
AB. Put the sharp end at A and mark an arc above and another arc below line segment AB.
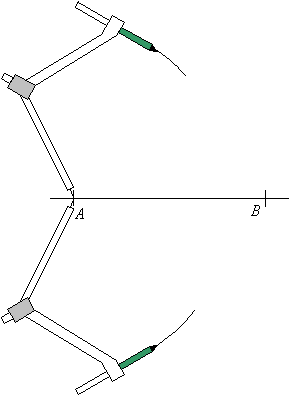
Step 2: Without changing the width of the compasses, put the sharp end at B and mark arcs above and below the line segment AB that will intersect with the arcs drawn in step 1.
Step 3: Join the two points where the arcs intersect with a straight line. This line is the perpendicular bisector of AB. P is the midpoint of AB.
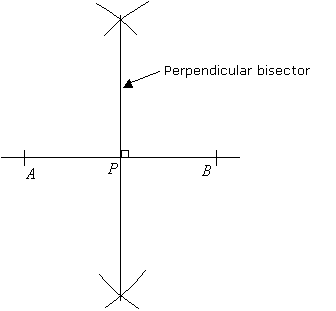
How to construct an isosceles triangle or a rhombus?
The above construction steps can also be used to construct an isosceles triangle or a rhombus.
Example:
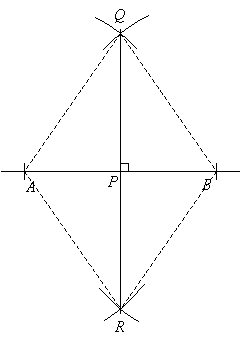
We have constructed 4 isosceles triangles; AQB, ARB, QAR and ARB. We have also constructed a rhombus AQBR.
How to construct a perpendicular bisector of a line segment?
- Draw a line segment.
- Set compasses to longer than half the length of line segment.
- Construct two arcs, one centered at each end, so that two intersections are created.
- Draw a line connecting the arc intersections.
How to bisect a line segment using only a compass and straightedge?
Uses of a Perpendicular Bisector
Constructing a Perpendicular Bisector with Isosceles Triangles
Forming either a Rhombus or a Kite and then joining opposite vertices with perpendicular diagonals bisecting each other.
How to Find the Midpoint of a Line Segment Using a Perpendicular Bisector
In this tutorial about geometric constructions, we walk through how to locate the mid-point of a line segment without a ruler, using a math compass and a straightedge. We can find the mid-point by draw a perpendicular bisector.
- Set your compass so that it is slightly larger than half the length of the segment.
- Place the compass at point A and draw a set of arcs above and below the line.
- Without changing the compass setting, place the compass at point B and draw a set of arcs intersecting the first set of arcs.
- Draw a point at each intersection of arcs.
- Connect the two points with a line.
- The point where the lines cross is the midpoint.
Constructing the Perpendicular Bisectors of the Sides of a Triangle
This video explains how to construct the perpendicular bisectors of the sides of a triangle and define the properties of the perpendicular bisectors of the sides of a triangle.
The circumcenter is the point of concurrency for the perpendicular bisectors of the sides of a triangle.
The circumcenter is the center of a circle that passes through the vertices of the triangle. The circumcenter is equidistant to the vertices.
We say the circle circumscribes the triangle.
| Check out our most popular games! | ||
|---|---|---|
 Fraction Concoction |
 Fact Family Game |
 Number Bond Garden |
 Online Addition Subtraction Game |
 Penguin Solitaire |
 Sawayama Solitaire |
 Ark Solitaire |
 Eldritch Invasion |
 Shenzhen Solitaire |
Check out more Solitaire games here.
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.