Percentage of a Number

Related Topics:
More Lessons for Arithmetic

Math Worksheets

To find the percentage of a number:

Step 1 : Change the percent to a fraction

Step 2 : Multiply the fraction by the number

Example:

Evaluate 25% of 200

Solution:

25% of 200 =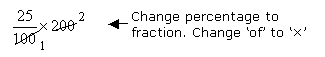

= 50

Example:

There are 25 marbles in a bag. If 20% of the marbles are red, how many of them are red?

Solution :

Number of red marbles = 20% of 25

=

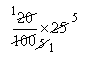
= 5

There are 5 red marbles in the bag.

Sometimes we may be given the percentage of a number and we are asked to find the number that represents the whole quantity. To find the whole quantity, we divide the given number by the given percentage.

Example:

If 25% of a number is 12, what is the number?

Solution:

Total quantity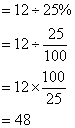

Example:

Amy saves RM 240, which is 12% of her salary. What is her salary?

Solution:

Salary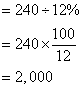

Her salary is RM 2,000

You can also find the percentage of a number by first changing the percent to a decimal

Step 1 : Change the percent to a decimal

Step 2 : Multiply the decimal by the number

The following video will give examples of using decimals to find the percentage of a number