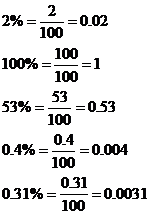Percent

Related Topics:
More Lessons for GRE Math

Math Worksheets

This lesson is part of a series of lessons for the quantitative reasoning section of the GRE revised General Test. In this lesson, we will learn:

• Percent
• Percents, Fractions, and Decimals
• Percent Problems
  • Using Percent Equation
  • Using Percent Proportion
• Percent Application Problems
• Percent Change

Percent

The term percent means per hundred, or hundredths. Percents are ratios that are often used to represent parts of a whole, where the whole is considered as having 100 parts.
• 15 percent means 15 part out of 100 parts, or
• 40 percent means 40 parts out of 100 parts, or
• 135 percent means 135 parts out of 100 parts, or

Note that the part is the numerator of the ratio and the whole is the denominator. It is possible for the part to be bigger than the whole. The whole is also called the base of the percent.

Percents, Fractions and Decimals

Percents are often written with the % symbol. We can convert percents to fractions and decimals, as follows.

Be careful not to confuse 0.01 with 0.01%. The percent symbol matters.
For example, 0.01 = 1% but 0.01% = 0.0001

This video contains a number of examples of converting percents into fractions and decimals.

Percent Problems

We will consider two methods that can be used to solve percent problems: Percent Equation and Percent Proportion.

Percent Equation

There are three types of percent problems. For example,

1) What is 65% of 80?
2) 52 is what percent of 80?
3) 52 is 65% of what number?

We will show how to use the percent equation to solve the percent problems. To set up the percent equation, we first identify some key words.

"of" translates to multiply "×".
"is" translates to equals "=".
"what" translates to a variable "n".
"p%" translates to the percent in decimal form.

Example:
1) What is 65% of 80?
n = 0.65 × 80 = 52

2) 52 is what percent of 80?
52 = p × 80
p = 80 ÷ 52 = 0.65 = 65%

3) 52 is 65% of what number?
52 = 0.65 × n
n = 52 ÷ 0.65 = 80

The following video shows examples of using the percent equation to solve problems.

This video explains how to solve the three types of percent problems using percent equations.

Percent Proportion

Percent problems involve three numbers that represent the percent, part and the base (or the whole). These three numbers form a percent proportion as follows:

Given any of the two numbers, we can then use the percent proportion to find the third number.

Sometimes, it can be difficult to know which number is the part and which number is the whole. One way would be to associate the word "is" with the part and the word "of" with the whole.

Example:
1. What is 65% of 80?


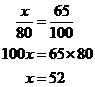
2. 52 is what percent of 80?


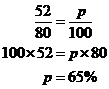
3. 52 is 65% of what number?

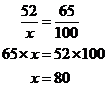
The following video shows how to solve Percent Problems using the Percent Proportion

Percent Application Problems

We will now look at some examples of percent application problems.

Example:
An investment in a mutual fund increased by 12% in a single day. If the value of the investment before the increase was $1,300, what was the value after the increase?

Solution:
The percent increase is 12%.
The value of the increase is
12% of $1,300 = 0.12 × $1,300 = $156.
The value of the investment after the change is
$1,300 + $156 = $1,456

A quantity may have several successive percent changes. The base of each successive percent change is the result of the preceding percent change.

Example:
The monthly enrollment at a preschool decreased by 8% during one month and increased by 6% during the next month. What was the cumulative percent change for the two months?

Solution:
Let E be the enrollment before the first month.
At the end of the first month, the enrollment would be
(100% - 8%) of E = 92% of E = 0.92E

At the end of the second month, the enrollment would be
(100% + 6%) of 0.92E = 106% of 0.92E = 1.06 × 0.92E = 0.9752E
0.9752 = 97.52% which is 2.48% less than 100%

Therefore, the cumulative percent change in the enrollment for the two months is a 2.48% decrease.

This video determines how much alcohol is in a 16 oz bottle of 60% rubbing alcohol.

This video determines if you score 54 out of 60 questions, what percentage did you score. This video determines if 2% of items are defective and there are 45 defective items, how many items were produced. This video determine the cost of an item when marked down 15% and with a tax rate of 8%.

Percent Change

When a quantity changes from an initial positive amount to another positive amount we can compute the amount of change as a percent of the initial amount. This is called percent change.

To find the percent change:

Step 1: Calculate the change in value (ending amount − beginning amount)
Step 2: Divide by the beginning amount (i.e. the value before the increase or decrease)
Step 3: Multiply by 100%

This video explains how to determine the percent of change. This video shows how to calculate a percent of increase from 3200 to 3400. This video shows how to calculate a percent of decrease from 80 to 65.