Illustrative Mathematics Grade 7, Unit 4, Lesson 7: One Hundred Percent

Related Pages
Illustrative Math
Grade 7

Lesson 7: One Hundred Percent

Let’s solve more problems about percent increase and percent decrease.

Illustrative Math Unit 7.4, Lesson 7 (printable worksheets)

Lesson 7 Summary

The following diagram shows how to find the percentage increase or decrease using a tape diagram.

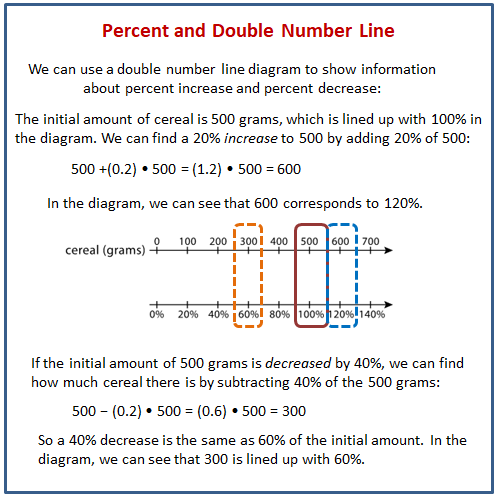
Lesson 7.1 Notice and Wonder: Double Number Line

What do you notice? What do you wonder?

• See Video for Whole Lesson

Lesson 7.2 Double Number Lines

For each problem, complete the double number line diagram to show the percentages that correspond to the original amount and to the new amount.

1. The gas tank in dad’s car holds 12 gallons. The gas tank in mom’s truck holds 50% more than that. How much gas does the truck’s tank hold?
2. At a movie theater, the size of popcorn bags decreased 20%. If the old bags held 15 cups of popcorn, how much do the new bags hold?
3. A school had 1,200 students last year and only 1,080 students this year. What was the percentage decrease in the number of students?
4. One week gas was $1.25 per gallon. The next week gas was $1.50 per gallon. By what percentage did the price increase?
5. After a 25% discount, the price of a T-shirt was $12. What was the price before the discount?
6. Compared to last year, the population of Boom Town has increased 25%.The population is now 6,600. What was the population last year?

Lesson 7.3 Representing More Juice

Two students are working on the same problem:
A juice box has 20% more juice in its new packaging. The original packaging held 12 fluid ounces. How much juice does the new packaging hold?
Here is how Priya set up her double number line.
Here is how Clare set up her double number line.
Do you agree with either of them? Explain or show your reasoning.

Are you ready for more?

Clare’s diagram could represent a percent decrease. Describe a situation that could be represented with Clare’s diagram.

• Show Answer

  Example:
  A toy is now sold at 20% less. The original price was $12. What is the new price?

Lesson 7.4 Protecting the Green Sea Turtle

Green sea turtles live most of their lives in the ocean, but come ashore to lay their eggs. Some beaches where turtles often come ashore have been made into protected sanctuaries so the eggs will not be disturbed.

1. One sanctuary had 180 green sea turtles come ashore to lay eggs last year. This year, the number of turtles increased by 10%. How many turtles came ashore to lay eggs in the sanctuary this year?
2. At another sanctuary, the number of nesting turtles decreased by 10%. This year there were 234 nesting turtles. How many nesting turtles were at this sanctuary last year?

Lesson 7 Practice Problems

1. A bakery used 25% more butter this month than last month. If the bakery used 240 kilograms of butter last month, how much did it use this month?
2. Last week, the price of oranges at the farmer’s market was $1.75 per pound. This week, the price has decreased by 20%. What is the price of oranges this week?
3. Noah thinks the answers to these two questions will be the same. Do you agree with him? Explain your reasoning.
   This year, a herd of bison had a 10% increase in population. If there were 550 bison in the herd last year, how many are in the herd this year?
   This year, another herd of bison had a 10% decrease in population. If there are 550 bison in the herd this year, how many bison were there last year?
   
4. Elena walked 12 miles. Then she walked 0.25 that distance. How far did she walk all together? Select all that apply.
   
5. A circle’s circumference is 600 m. What is a good approximation of the circle’s area?
   A. 300 m²
   B. 3,000 m²
   C. 30,000 m²
   D. 300,000 m²
   
6. The equation d = 3t represents the relationship between the distance (d) in inches that a snail is from a certain rock and the time (t) in minutes.
   a. What does the number 3 represent?
   b. How many minutes does it take the snail to get 9 inches from the rock?
   c. How far will the snail be from the rock after 9 minutes?

The Open Up Resources math curriculum is free to download from the Open Up Resources website and is also available from Illustrative Mathematics.

Try the free Mathway calculator and problem solver below to practice various math topics. Try the given examples, or type in your own problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.