Illustrative Mathematics Unit 6.1, Lesson 7: From Parallelograms to Triangles

Related Topics:
Math Worksheets

Learn about comparing the area of parallelograms and the area of triangles. After trying the questions, click on the buttons to view answers and explanations in text or video.

Return to the list of Illustrative Math lessons

Same Parallelograms, Different Bases
Let’s compare parallelograms and triangles.

Illustrative Math Unit 6.1, Lesson 7 (printable worksheets)

7.1 - Same Parallelograms, Different Bases

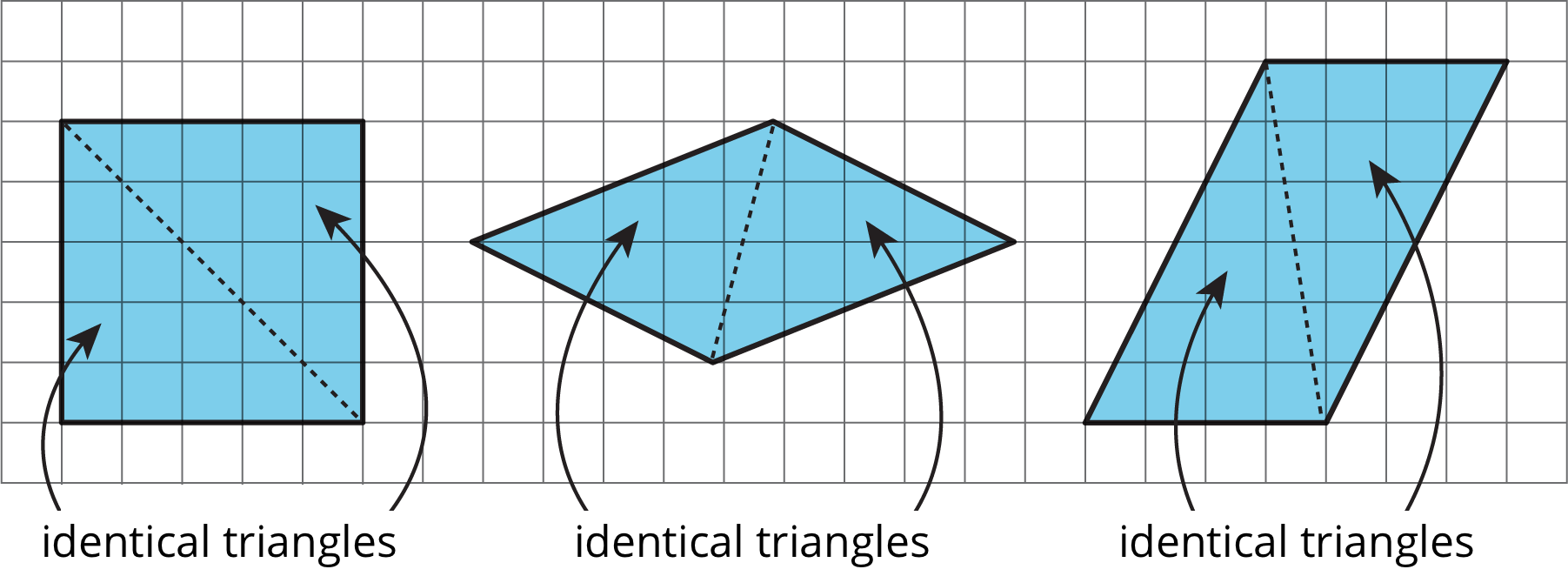
Here are two copies of a parallelogram. Each copy has one side labeled as the base b and a segment drawn for its corresponding height and labeled h.

1. The base of the parallelogram on the left is 2.4 centimeters; its corresponding height is 1 centimeter. Find its area in square centimeters.

2. The height of the parallelogram on the right is 2 centimeters. How long is the base of that parallelogram? Explain your reasoning.

• Answers

  1. 2.4 cm × 1 cm = 2.4 square cm

  2. This parallelogram is identical to the one on the left, so its area is the same.
  2.4 square cm = b × 2 cm
  b = 1.2 cm

• See Video 1 for Whole Lesson
• See Video 2 for Whole Lesson

7.2 - A Tale of Two Triangles (Part 1)

Two polygons are identical if they match up exactly when placed one on top of the other.

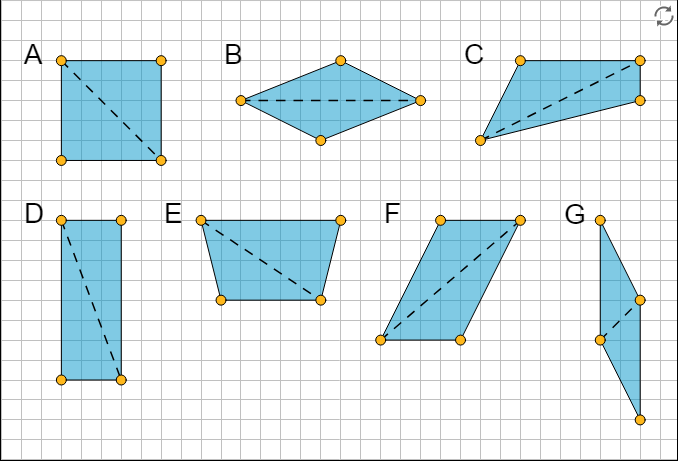
1. Open the applet. Draw one line segment to decompose each of the following polygons into two identical triangles, if possible. If you choose to, you can also draw the triangles.

2. Which quadrilaterals can be decomposed into two identical triangles?

3. Study the quadrilaterals that were, in fact, decomposable into two identical triangles. What do you notice about them? Write a couple of observations about what these quadrilaterals have in common.

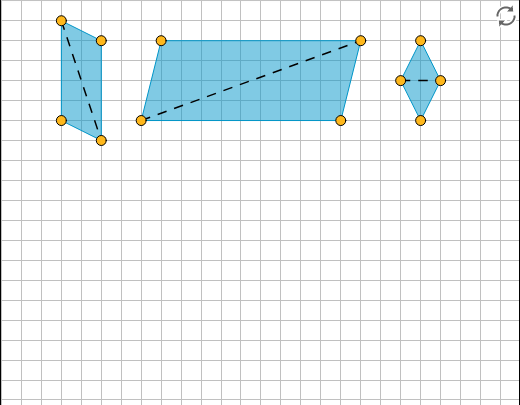
Open the next applet. Draw some other types of quadrilaterals that are not already shown. Try to decompose them into two identical triangles. Can you do it? Come up with a general rule about what must be true if a quadrilateral can be decomposed into two identical triangles.

• See Possible Answers

  1. These are examples of how the quadrilaterals can be decomposed into triangles by connecting opposite vertices. However, triangles from the same quadrilateral are not always identical. See the answers to the following questions for more detail.
  

  2. A, B, D, F, and G can be decomposed into two identical triangles. C and E cannot.

  3. A, B, D, F, and G have two pairs of parallel sides, equal opposite sides, and equal opposite angles, while C and E do not.

  
  These are examples of additional quadrilaterals that can be decomposed into two identical triangles. Based on this and the previous answers, we can conclude that for a quadrilateral to be decomposable into two identical triangles it must be a parallelogram.

7.3 - A Tale of Two Triangles (Part 2)

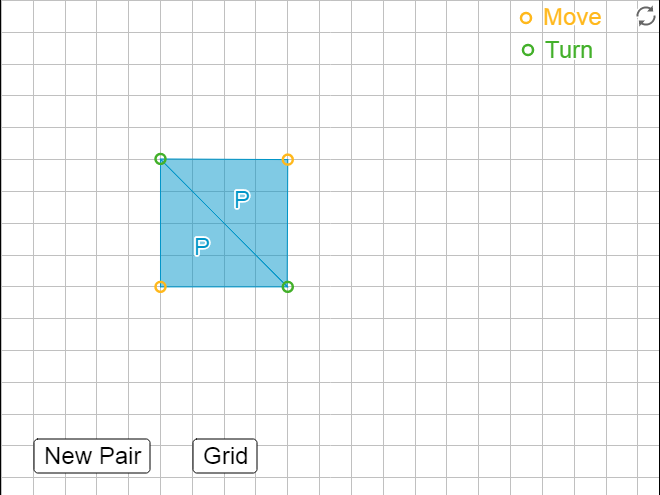
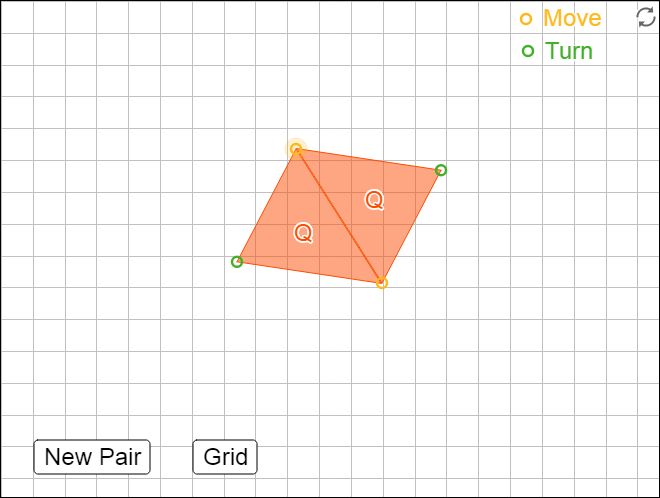
3. This applet has eight pairs of triangles. Choose 1–2 pairs of triangles. Use them to help you answer the following questions.

1. Which pair(s) of triangles do you have? _________________ Can each pair of triangles be composed into:
a. a rectangle?
b. a parallelogram?

2. Check the other pairs. Complete each of the following statements with the words "all", "some", or "none". Sketch 1–2 examples to illustrate each completed statement.
a. ________________ of these pairs of identical triangles can be composed into a rectangle.
b. ________________ of these pairs of identical triangles can be composed into a parallelogram.

• See Possible Answers

  
  Pair P can be composed into a square, which has all the properties of a rectangle or a parallelogram. (See this link for more information about how squares, rectangles, and parallelograms are related.)

  
  Pair Q can be composed into a parallelogram.

  Some of these pairs of identical triangles can be composed into a rectangle.
  All of these pairs of identical triangles can be composed into a parallelogram.

Lesson 7 Summary

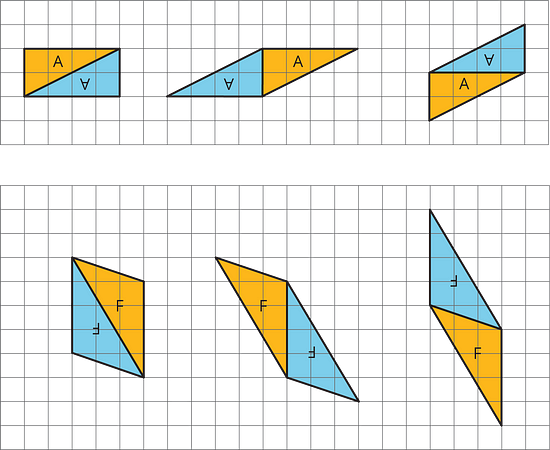
A parallelogram can always be decomposed into two identical triangles by a segment that connects opposite vertices.

• Show Parallelograms
  

Going the other way around, two identical copies of a triangle can always be arranged to form a parallelogram, regardless of the type of triangle being used.

To produce a parallelogram, we can join a triangle and its copy along any of the three sides, so the same pair of triangles can make different parallelograms.

Here are examples of how two copies of both Triangle A and Triangle F can be composed into three different parallelograms.

• Show Parallelograms
  

• Show Parallelograms
  

This special relationship between triangles and parallelograms can help us reason about the area of any triangle.

Practice Problems

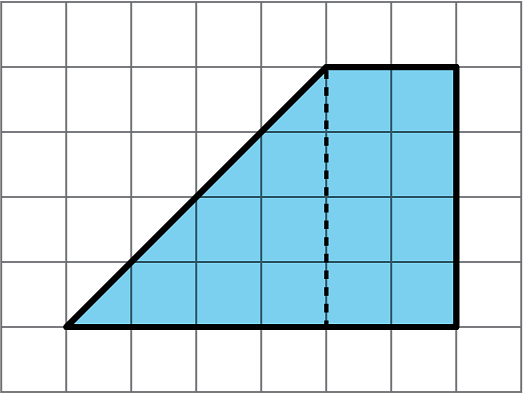
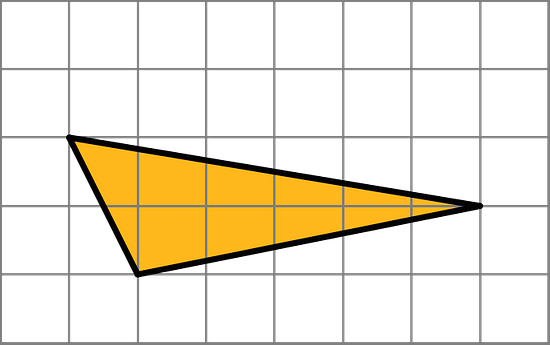
1. To decompose a quadrilateral into two identical shapes, Clare drew a dashed line as shown in the diagram.

• Show Figure
  

A: Clare said the that two resulting shapes have the same area. Do you agree? Explain your reasoning.
B: Did Clare partition the figure into two identical shapes? Explain your reasoning.

• Answers

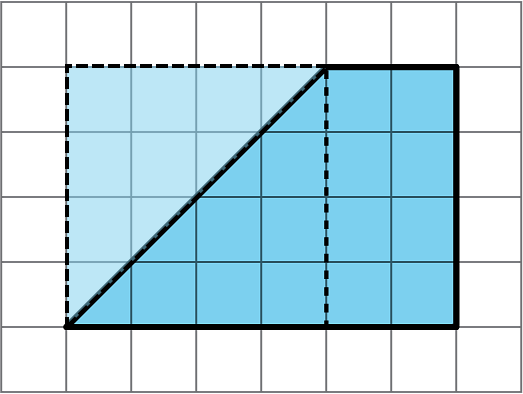
  A: The two shapes do have the same area. The area of the rectangle is 4 × 2 = 8 square units, while the area of the triangle is half the area of a square that is 4 by 4 units, as shown below, so its area is ½ × (4 × 4) = 8 square units.
  

  B: These are not two identical shapes. One is a triangle and the other is a rectangle. The original quadrilateral is not a parallelogram either, so it may or may not be possible to divide the original quadrilateral into identical halves.

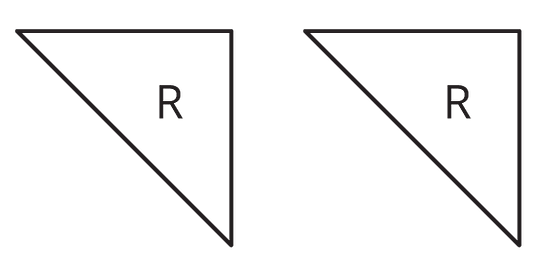
2. Triangle R is a right triangle. Can we use two copies of Triangle R to compose a parallelogram that is not a square?

• Show Figures
  

If so, explain how or sketch a solution. If not, explain why not.

• Answers

  

  It is possible to use two copies of Triangle R to compose a parallelogram that is not a square.

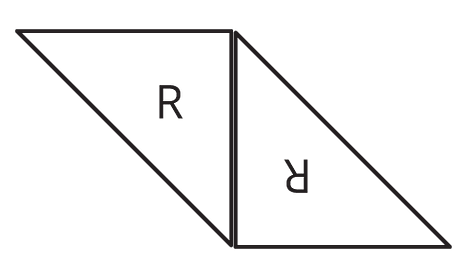
3. Two copies of this triangle are used to compose a parallelogram. Which parallelogram cannot be a result of the composition? If you get stuck, consider using tracing paper.

• Show Figures
  

• Answers

  

  A, B, and D can all be composed out of copies of this triangle, as seen by the triangle covering exactly half of each of these parallelograms. C cannot be composed out of copies of this triangle, as the remaining unshaded area is not a triangle.

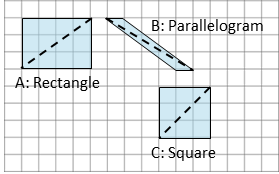
4. A: On the grid, draw at least three different quadrilaterals that can each be decomposed into two identical triangles with a single cut (show the cut line). One or more of the quadrilaterals should have non-right angles.

• Show Grid
  

B: Identify the type of each quadrilateral.

• See Possible Answers

  

  All parallelograms are quadrilaterals that can be decomposed into two identical triangles with a single cut. Squares and rectangles have all the properties of parallelograms.

  A is a rectangle. B is a parallelogram with non-right angles. C is a square.

5. A: A parallelogram has a base of 9 units and a corresponding height of ⅔ units. What is its area?
B: A parallelogram has a base of 9 units and an area of 12 square units. What is the corresponding height for that base?
C: A parallelogram has an area of 7 square units. If the height that corresponds to a base is ¼ unit, what is the base?

• Answers

  A: A = b · h
  A = 9 units · ⅔ units
  A = 6 square units

  B: A = b · h
  12 square units = 9 units · h
  h = 12 square units ÷ 9 units
  h = 1⅓ units

  C: A = b · h
  7 square units = b · ¼ unit
  b = 7 square units ÷ ¼ unit
  b = 28 units

6. List all segments that could represent a corresponding height if the side n is the base.

• Show Figure
  

• Answers

  g and h are perpendicular to the base n and could represent its corresponding height.

The Open Up Resources math curriculum is free to download from the Open Up Resources website and is also available from Illustrative Mathematics.

Try the free Mathway calculator and problem solver below to practice various math topics. Try the given examples, or type in your own problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.