OML Search

Illustrative Mathematics Unit 6.1, Lesson 4: Parallelograms

Related Topics:
Math Worksheets




Learn what is and is not a parallelogram and how to find the area of a parallelogram. After trying the questions, click on the buttons to view answers and explanations in text or video.

Return to the list of Illustrative Math lessons


Parallelograms
Let’s investigate the features and area of parallelograms.

Illustrative Math Unit 6.1, Lesson 4 (printable worksheets)

4.1 - Features of a Parallelogram

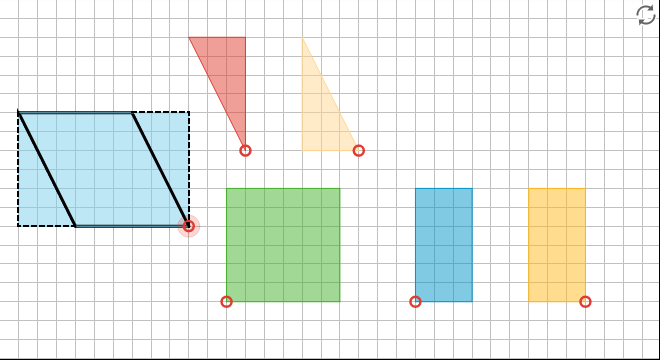
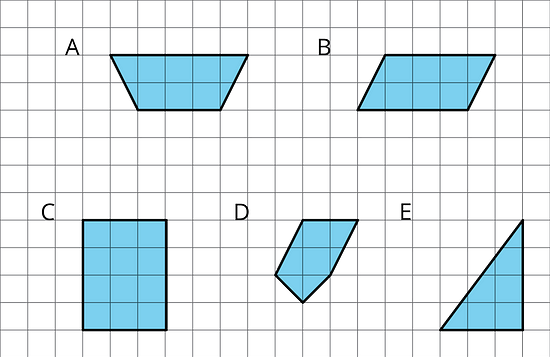
Figures A, B, and C are parallelograms. Figures D, E, and F are not parallelograms.

Six figures on a grid labeled A--F.

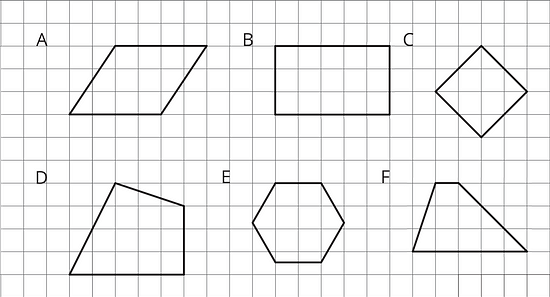
Study the examples and non-examples. What do you notice about:

1. the number of sides that a parallelogram has?
2. opposite sides of a parallelogram?
3. opposite angles of a parallelogram?

Based on your observations, how would you define a parallelogram?

  • What Is A Parallelogram?

    A parallelogram has all of the following properties:

    • Is a polygon with 4 sides
    • Both pairs of opposite sides are parallel, i.e. they never intersect
    • Opposite sides have equal length
    • Opposite angles have equal measure

    Squares and rectangles are also parallelograms as they have all these properties.

    Figure D is not a parallelogram because it does not have parallel opposite sides.
    Figure E is not a parallelogram because it has 6 sides.
    Figure F is not a parallelogram because it does not have two pairs of parallel opposite sides.

  • See Video 1 for Whole Lesson
  • See Video 2 for Whole Lesson




4.2 - Area of a Parallelogram

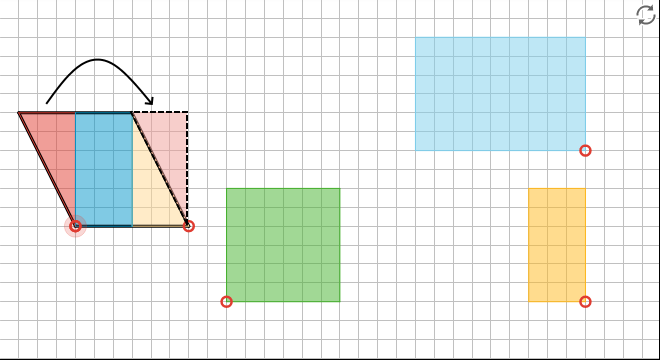
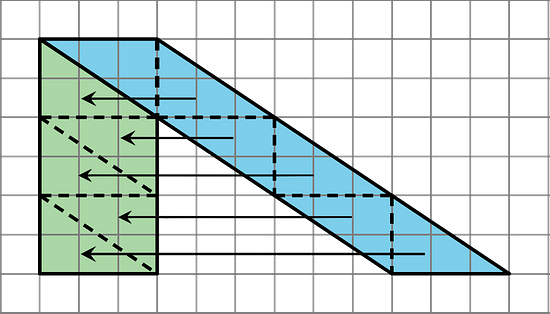
1. Open the applet. Find the area of the parallelogram and explain your reasoning. Each shape can be moved by dragging the red points on their vertices.

2. Open the next applet. This parallelogram can be changed by dragging the green points on its vertices. For any parallelogram that you make, find its area and explain your reasoning.

3. If you used the polygons on the side, how were they helpful? If you did not, could you use one or more of the polygons to show another way to find the area of the parallelogram?

  • See Possible Answers

    A parallelogram on a grid. The parallelogram has been decomposed into 1 rectangle 3 by 6 square units and 2 right triangles. The 2 right triangles have been rearranged into 1 rectangle 3 by 6 square units.

    1. A parallelogram can be decomposed into rectangles and right triangles, and then rearranged into rectangles whose area can be calculated from their side lengths.
    The blue rectangle has an area of 3 × 6 = 18 square units. The rectangle made from the 2 right triangles also has an area of 18 square units. The total area of the parallelogram is 18 + 18 = 36 square units.

    A parallelogram on a grid. The parallelogram has been enclosed with a rectangle 9 by 6 square units. Extra regions in the form of 2 right triangles which each have a base length of 3 and a height of 6 have been marked with dashed lines for subtraction.

    Alternatively, the parallelogram can be enclosed in a larger rectangle and the combined area of the extra regions can be subtracted.
    The blue rectangle has an area of 9 × 6 = 54 square units. The extra regions can be rearranged into a rectangle with an area of 18 square units. The total area of the parallelogram is 54 - 18 = 36 square units.

    For questions 2-3, the process used for question 1 can be used to find the area of the parallelograms that you make with the applet.


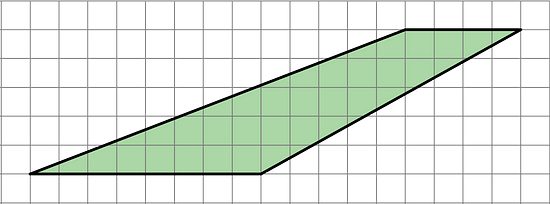
4.3 - Lots of Parallelograms

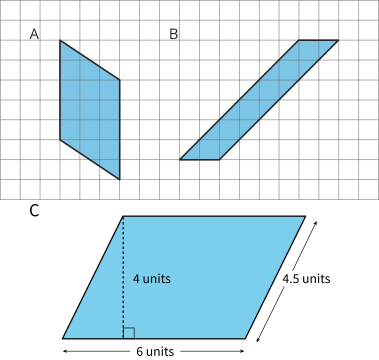
Find the area of the following parallelograms. Show your reasoning.

  • See Possible Answers

    Three figures. Two figures are on a grid: parallelogram A and parallelogram B. Parallelogram A has base length 5 units and height 3 units. Parallelogram B has base length 2 units and height 6 units. Parallelogram C is not on a grid. Parallelogram C has base 6 units, height 4 units, and diagonal length 4.5 units. Figure A has been decomposed into a rectangle and 2 right triangles. Figure B has been enclosed in a rectangle and the extra regions for subtraction have been indicated with dashed lines.

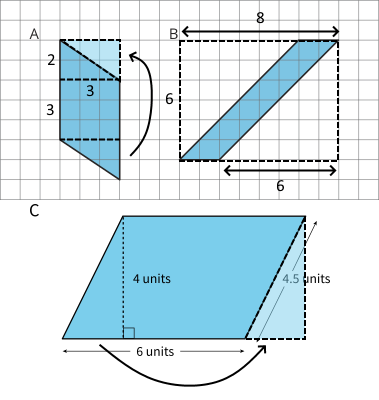
    Parallelogram A can be decomposed and rearranged as shown into a rectangle 5 by 3 units. The area of this rectangle, and therefore the area of the original Parallelogram A, is 5 × 3 = 15 square units.

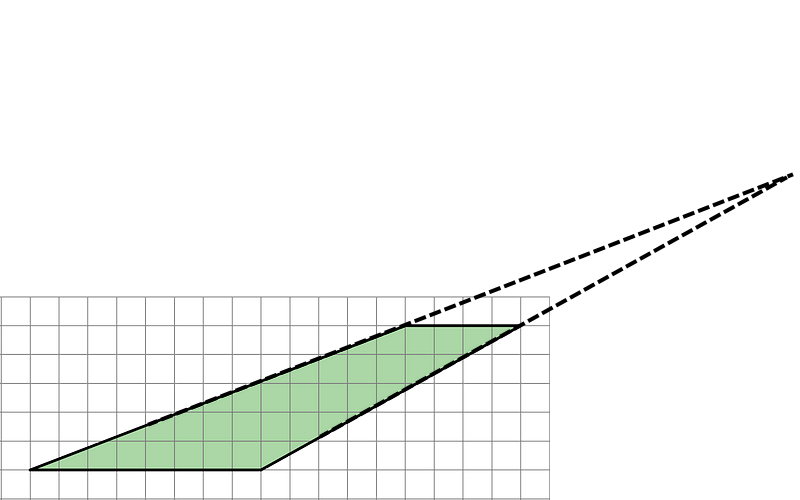
    Parallelogram B can be enclosed in a larger rectangle 6 by 8 units. The extra triangular regions can be rearranged into a square 6 by 6 units. Hence, the area of Parallelogram B is (6 × 8) - (6 × 6) = 12 square units.
    For this parallelogram, enclosing and subtracting will take fewer steps than decomposing and rearranging.

    Parallelogram C can be decomposed and rearranged into a rectangle 4 by 6 units. Note that the base length of 6 units is unchanged. The area of Parallelogram C is 4 × 6 = 24 square units.
    Since the diagonals are parallel, the right triangles from decomposing the parallelogram will match up with each other, even when there is no grid to verify this.
    Note also that the diagonal length of 4.5 units was not necessary to find the area.




Lesson 4 Summary

A parallelogram has all of the following properties:

  • Is a quadrilateral, i.e. it is a polygon with 4 sides
  • Both pairs of opposite sides are parallel, i.e. they never intersect
  • Opposite sides have equal length
  • Opposite angles have equal measure

Two parallelograms demonstrating the properties of a parallelogram.

There are several strategies for finding the area of a parallelogram.

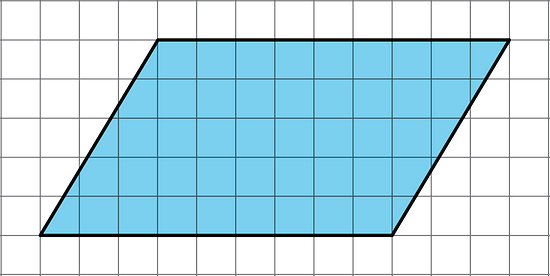
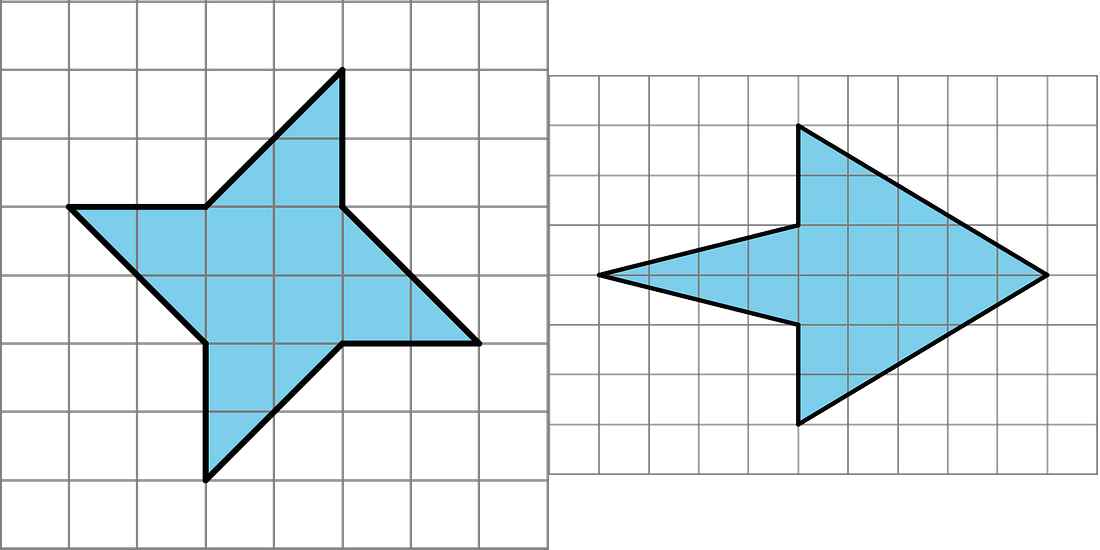
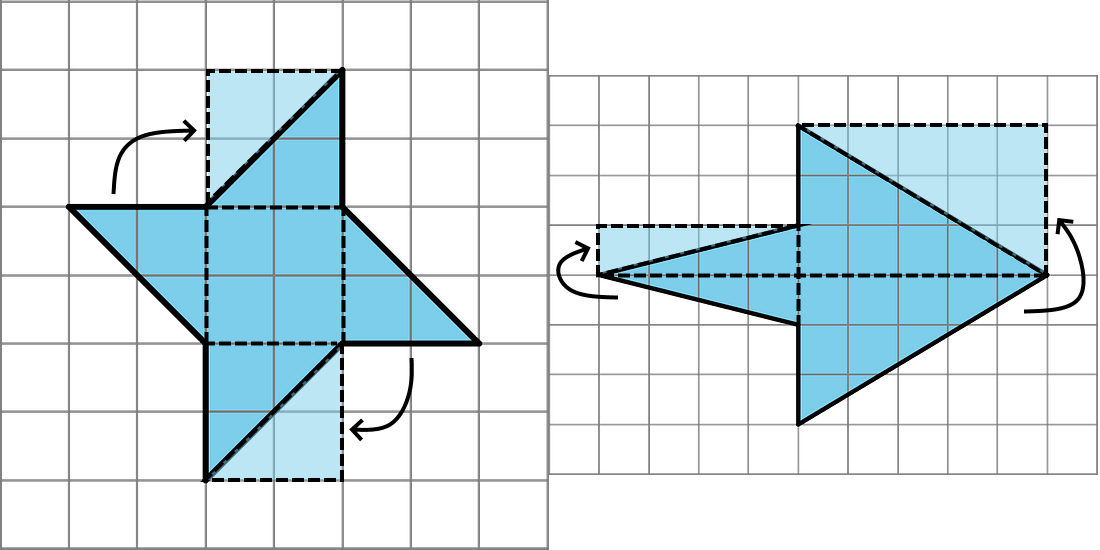
  • We can decompose and rearrange a parallelogram to form a rectangle. The image below shows three ways to decompose and rearrange a parallelogram:

    Three identical parallelograms with horizontal sides that are four units long, drawn in grids. The first parallelogram has a perpendicular segment extending from 2 units in from the top left down to the vertex of the bottom horizontal side. An arrow extends from the resulting triangle to the opposite side of the parallelogram to create a rectangle measuring 4 units wide and 3 units high. The second parallelogram has a perpendicular segment extending from 2 units in from the bottom right up to the vertex of the top horizontal side. An arrow extends from the resulting triangle to the opposite side of the parallelogram to create a rectangle measuring 4 units wide and 3 units high. The third parallelogram has a perpendicular segment extending from 3 units in from the bottom right up to the vertex of the top horizontal side. An arrow extends from the resulting shape to the opposite side of the parallelogram to create a rectangle measuring 4 units wide and 3 units high.

  • We can enclose the parallelogram and then subtract the area of the two triangles in the corner.

    A parallelogram with base length 4 units and height 3 units is enclosed with two right triangles to make a rectangle 6 by 3 units. The right triangles are rearranged to make a small rectangle 2 by 3 units, whose area can be subtracted from the larger rectangle to find the area of the parallelogram.


Both of these methods will work for any parallelogram.

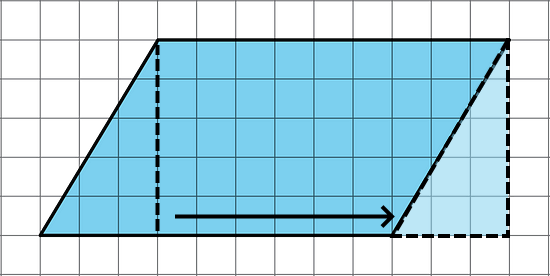
For some parallelograms, however, the process of decomposing and rearranging requires a lot more steps than if we enclose the parallelogram with a rectangle and subtract the combined area of the two triangles in the corners. Here is an example.

Practice Problems

1. Select all of the parallelograms. For each figure that is not selected, explain how you know it is not a parallelogram.

  • Answers

    Figure A is not a parallelogram because it has two non-parallel sides.

    Figure B is a parallelogram.

    Figure C is a parallelogram. Squares and rectangles have all the properties of parallelograms.

    Figure D is not a parallelogram because it is not a quadrilateral.

    Figure E is not a parallelogram because it is not a quadrilateral.


2. Decompose and rearrange this parallelogram to make a rectangle. What is the area of the parallelogram? Explain your reasoning.

  • Answers

    A parallelogram on a grid with base length 9 units and height 5 units. The parallelogram has been decomposed to form a rectangle 9 by 5 units.

    This parallelogram can be decomposed and rearranged to make a rectangle 9 units by 5 units. The area of this rectangle, and therefore the area of the parallelogram, is 9 × 5 = 45 square units.


3. Find the area of the parallelogram.

  • Answers

    A parallelogram with one side labeled 3.2 centimeters, and another side labeled 10 centimeters. A dashed line perpendicular to the 10 centimeter sides is labeled 3 centimeters. The parallelogram has been decomposed and rearranged into a rectangle 10 by 3 centimeters.

    This parallelogram can be decomposed and rearranged to make a rectangle 10 centimeters by 3 centimeters. The area of this rectangle, and therefore the area of the parallelogram, is 10 × 3 = 30 square units.
    Note that the diagonal length of 3.2 centimeters was not used to find the area.


4. Explain why this quadrilateral is not a parallelogram.

  • Answers

    This quadrilateral is not a parallelogram because one pair of opposite sides is not parallel, as shown:

    A quadrilateral with a bottom side length of 8 units, a top side length of 4 units. The left side ascends 5 units while moving right 13 units, and the right side ascends 5 units while moving right 9 units. The diagonal sides have been extended to show where they would intersect outside the grid.


5. Find the area of each shape. Show your reasoning.

  • Answers

    Two figures. Left figure: A shape with eight sides. Four sides are straight sides and extend left, right, up and, down for 2 units each. The remaining sides are angled sides connecting each of the straight sides to the next. The shape is a total of 6 units tall and 6 units wide. The figure has been decomposed and rearranged into a rectangle 2 by 6 units. Right figure: A shape with six sides. It is 9 units long and six units wide at its widest point. Two vertical sides connect four sloped sides, which meet at either end of the shape. The figure has been decomposed into two rectangles, one 4 by 1 units and one 5 by 3 units.

    Both figures can be decomposed and rearranged into rectangles whose area can be found by multiplying the side lengths.

    The figure on the left can be decomposed and rearranged into a rectangle 2 units by 6 units. The area of the rectangle, and therefore the area of the figure, is 2 × 6 = 12 square units.

    The figure on the right can be decomposed and rearranged into two rectangles. One rectangle has an area of 1 × 4 = 4 square units, and the other has an area of 3 × 5 = 15 square units. The total area of the figure is 4 + 15 = 19 square units.


6. Find the areas of the rectangles with the following side lengths.

a. 5 in and ⅓ in
b. 5 in and 4⁄3 in
c. 5⁄2 in and 4⁄3 in
d. 7⁄6 in and 6⁄7 in

  • Answers

    a. 5 in × ⅓ in = 5⁄3 square inches = 12⁄3 square inches
    b. 5 in × 4⁄3 in = 20⁄3 square inches = 62⁄3 square inches
    c. 5⁄2 in × 4⁄3 in = 10⁄3 square inches = 31⁄3 square inches
    d. 7⁄6 in × 6⁄7 in = 1 square inch




The Open Up Resources math curriculum is free to download from the Open Up Resources website and is also available from Illustrative Mathematics.

Try the free Mathway calculator and problem solver below to practice various math topics. Try the given examples, or type in your own problem and check your answer with the step-by-step explanations.
Mathway Calculator Widget


OML Search


We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.



 
Back to Top | Interactive Zone | Home

Copyright © 2005, 2024 - OnlineMathLearning.com.
Embedded content, if any, are copyrights of their respective owners.