Illustrative Mathematics Unit 6.1, Lesson 14: Nets and Surface Area

Learn about matching nets to their polyhedra and using nets to find the surface area of a polyhedron. After trying the questions, click on the buttons to view answers and explanations in text or video.

Return to the list of Illustrative Math lessons

Nets and Surface Area
Let’s use nets to find the surface area of polyhedra.

Illustrative Math Unit 6.1, Lesson 14 (printable worksheets)

14.1 - Matching Nets

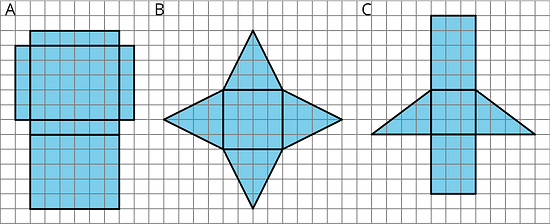
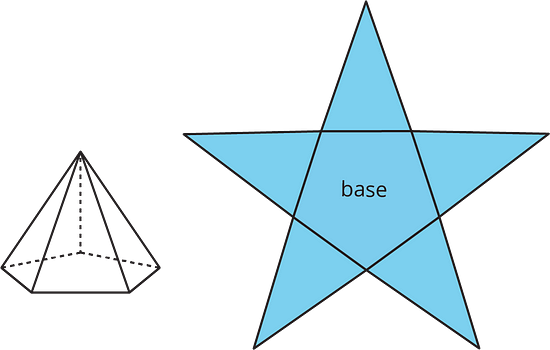
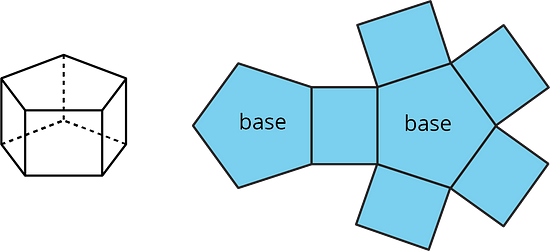
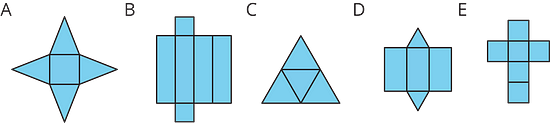
Each of the following nets can be assembled into a polyhedron. Match each net with its corresponding polyhedron, and name the polyhedron. Be prepared to explain how you know the net and polyhedron go together.

 

• Show Answers

  A: 3 - Square pyramid, formed from a square base and 4 triangles.
  B: 2 - Square prism, formed from 2 square bases and 4 rectangles.
  C: 4 - Triangular pyramid (tetrahedron), formed from a triangular base and 3 triangles.
  D: 5 - Triangular prism, formed from 2 triangular bases and 3 rectangles.
  E: 1 - Cube, formed from 6 squares.

• See Video 1 for Whole Lesson

• See Video 2 for Whole Lesson

14.2 - Using Nets to Find Surface Area

Your teacher will give you the nets of three polyhedra to cut out and assemble. Alternatively, you may print out the following nets.

• Show Image
  

1. Name the polyhedron that each net would form when assembled.

2. Cut out your nets and use them to create three-dimensional shapes.

3. Find the surface area of each polyhedron. Explain your reasoning clearly.

• Show Hints
  1. Recall the definitions of a prism and a pyramid, and how these are named.
  3. A net allows us to see all the faces of a polygon at once. To find the surface area of a polyhedron from its net, find the total area of all the polygons in the net.

• Show Possible Answers

  1. A forms a rectangular prism. B forms a square pyramid. C forms a triangular prism (with right triangular bases).

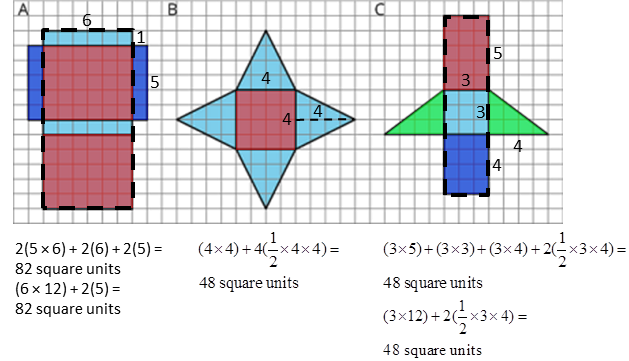
  2. A net allows us to see all the faces of a polygon at once. To find the surface area of a polyhedron from its net, find the total area of all the polygons in the net. In each of these nets, polygons with the same area have been shaded the same color. To simplify calculations, polygons can also be combined to calculate area, as indicated by the dashed outlines in nets A and C.

  
   
  

  A: 2(5 × 6) + 2(6) + 2(5) = 82 square units
  OR (6 × 12) + 2(5) = 82 square units

  B: (4 × 4) + 4(½ × 4 × 4) = 48 square units

  C: (3 × 5) + (3 × 3) + (3 × 4) + 2(½ × 3 × 4) = 48 square units
  OR (3 × 12) + 2(½ × 3 × 4) = 48 square units

  Other strategies are also possible.

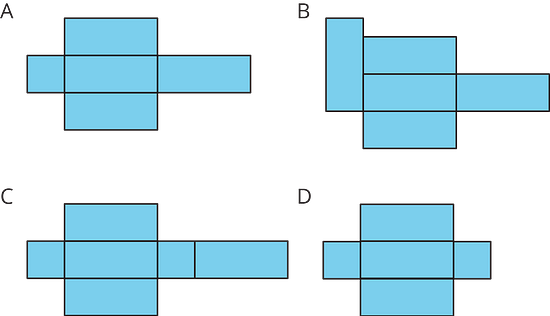
1. For each net, decide if it can be assembled into a rectangular prism.

• Show Image
  

2. For each net, decide if it can be assembled into a triangular prism.

• Show Image
  

• Show Answers

  1. Only C can be folded into a rectangular prism.
     A has a square face which does not form a pair with any other face.
     B has a rectangle which contacts more than one other rectangle along one of its edges, and so cannot be folded into a polyhedron.
     D does not have enough faces to form a closed polyhedron.

  2. Only D can be folded into a triangular prism.
     A is impossible to fold such that the triangles are on opposite sides.
     B and C are impossible to fold such that all the sides of each face are in contact with another face.
     

Lesson 14 Summary

A net of a pyramid has one polygon that is the base. The rest of the polygons are triangles. A pentagonal pyramid and its net are shown here.

• Show Image
  

A net of a prism has two copies of the polygon that is the base. The rest of the polygons are rectangles. A pentagonal prism and its net are shown here.

• Show Image
  

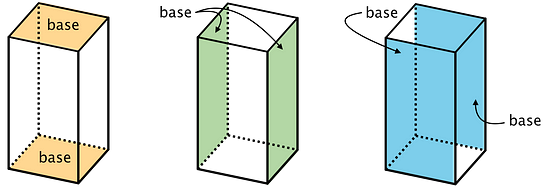
In a rectangular prism, there are three pairs of parallel and identical rectangles. Any pair of these identical rectangles can be the bases.

• Show Image
  

Because a net shows all the faces of a polyhedron, we can use it to find its surface area.
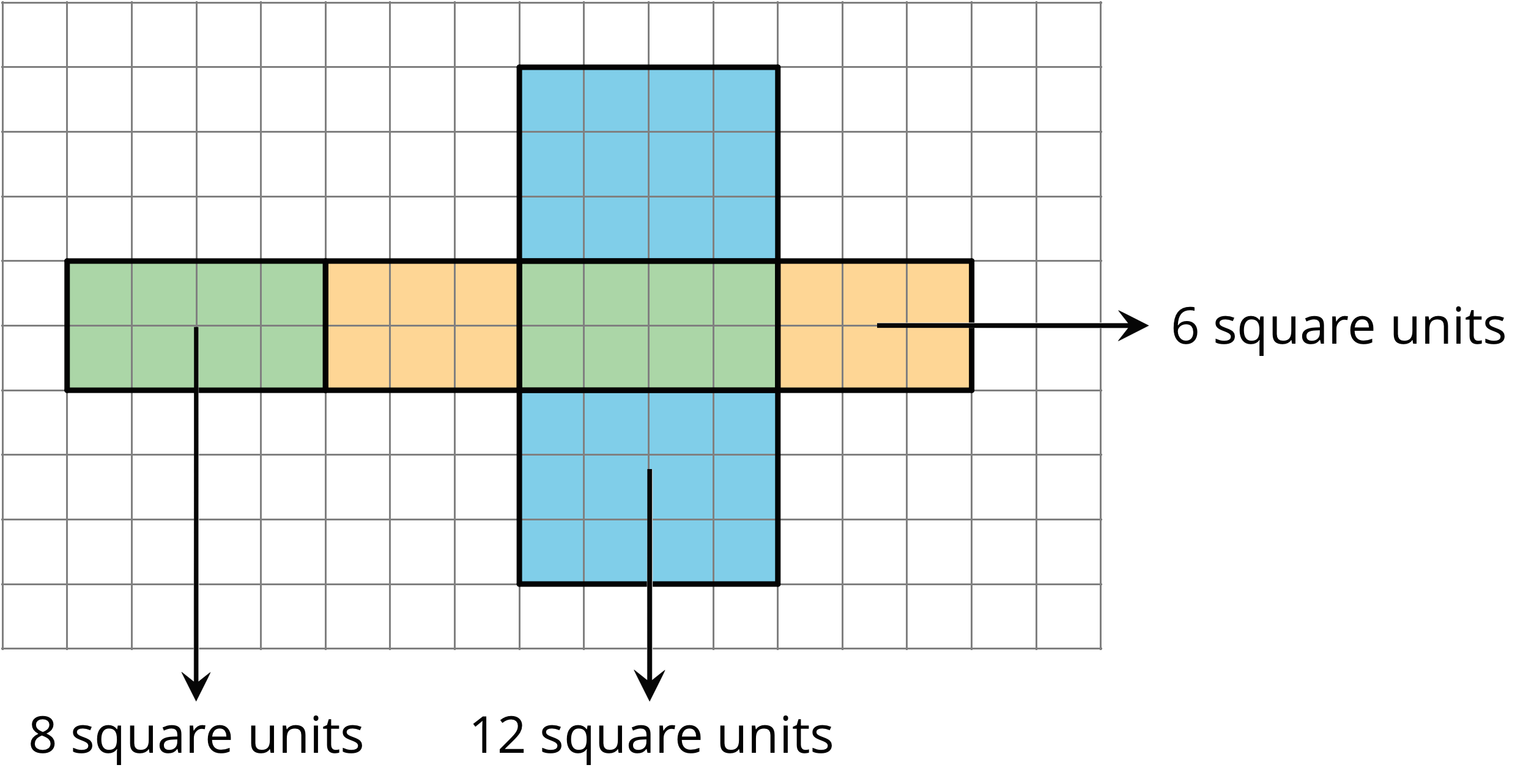
For instance, the net of a rectangular prism shows three pairs of rectangles: 4 units by 2 units, 3 units by 2 units, and 4 units by 3 units.

• Show Image
  

The surface area of the rectangular prism is 52 square units because 8 + 8 + 6 + 6 + 12 + 12 = 52.

Practice Problems

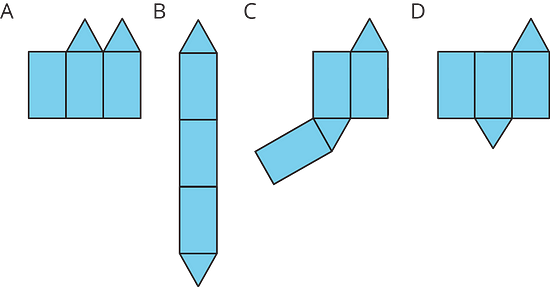
1. Can the following net be assembled into a cube? Explain how you know. Label parts of the net with letters or numbers if it helps your explanation.

• Show Image
  

• Show Answers
  

  This net cannot be assembled into a cube. Squares 1 and 6 will always overlap each other.

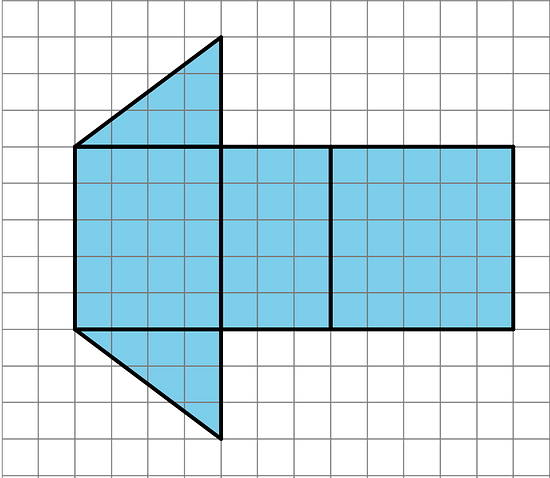
2. a. What polyhedron can be assembled from this net? Explain how you know.
   b. Find the surface area of this polyhedron. Show your reasoning.

• Show Image
  

• Show Possible Answers

  a. This net can be assembled into a triangular prism. There are two congruent triangles which are the bases, and three rectangles for connecting the bases.

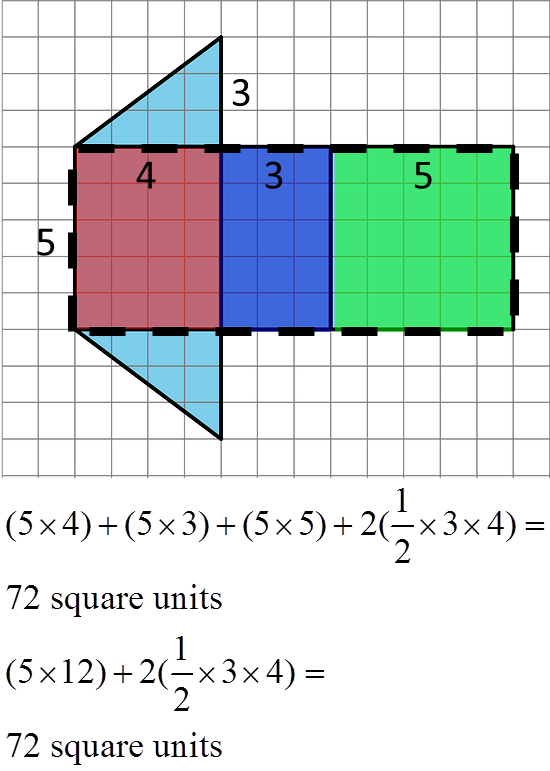
  b. Faces which have the same area have been shaded the same color. The contiguous rectangular faces can also be considered as one large rectangle to simplify calculations.

  
   
  

  The area of this polyhedron is (5 × 4) + (5 × 3) + (5 × 5) + 2(½ × 3 × 4) = 72 square units
  OR (5 × 12) + 2(½ × 3 × 4) = 72 square units

  Other strategies are also possible.

3. Here are two nets. Mai said that both nets can be assembled into the same triangular prism. Do you agree? Explain or show your reasoning.

• Show Image
  

• Show Answers

  Mai is correct. In both nets, the rectangles can be folded to touch every edge of both triangular bases.

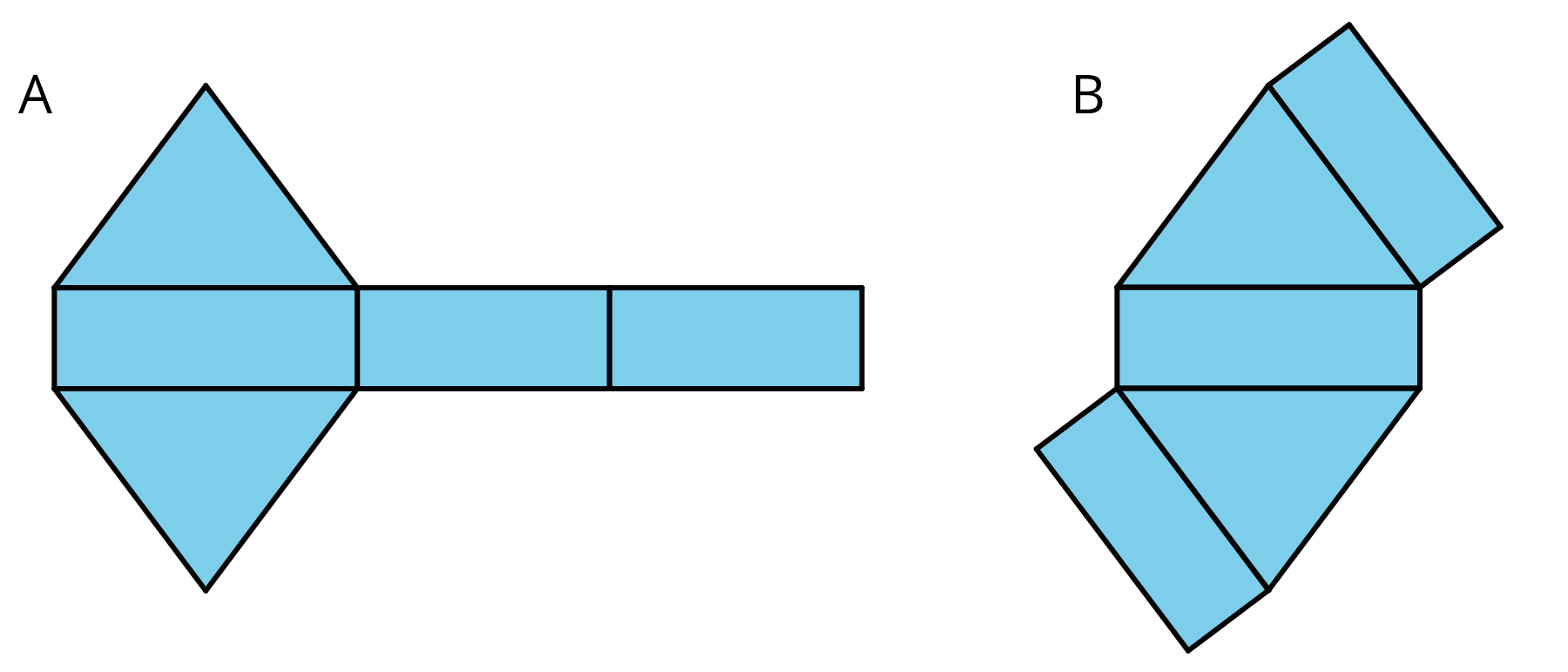
4. Here are two three-dimensional figures.

• Show Image
  

Tell whether each of the following statements describes Figure A, Figure B, both, or neither.

a. This figure is a polyhedron.
b. This figure has triangular faces.
c. There are more vertices than edges in this figure.
d. This figure has rectangular faces.
e. This figure is a pyramid.
f. There is exactly one face that can be the base for this figure.
g. The base of this figure is a triangle.
h. This figure has two identical and parallel faces that can be the base.

• Show Answers

  a. Both - both figures are polyhedra.
  b. Both - Figure A is a triangular prism, and Figure B is a triangular pyramid.
  c. Neither - both figures have more edges than vertices.
  d. Figure A
  e. Figure B
  f. Neither - Figure A is a prism and has two bases. Any face of a triangular pyramid like Figure B can be its base.
  g. Both - Figure A is a triangular prism with two triangular bases, and Figure B is a triangular pyramid with a triangular base.
  h. Figure A - this is a feature of a prism.

5. Select all units that can be used for surface area. Explain why the others cannot be used for surface area.

A. square meters
B. feet
C. centimeters
D. cubic inches
E. square inches
F. square feet

• Show Answers

  A, E, and F are all units that can be used for surface area, as they are square units (two-dimensional).
  B and C cannot be used as they are units of length. D cannot be used as it is a cubic unit, a unit of volume (three-dimensional).

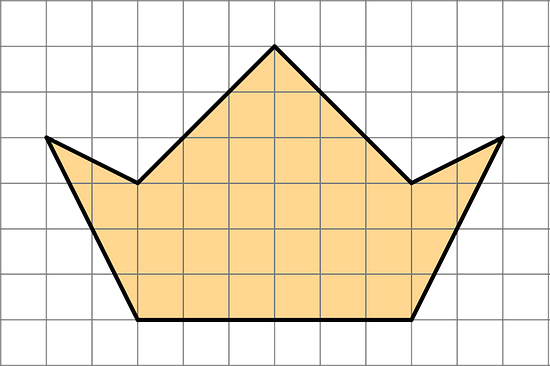
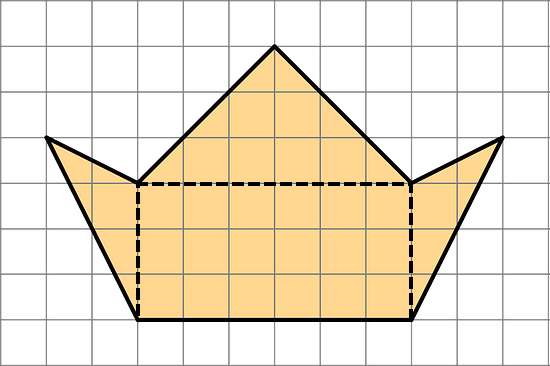
6. Find the area of this polygon. Show your reasoning.

• Show Image
  

• Show Answers
  

  The polygon can be divided into 3 triangles and 1 rectangle.

  The total area of these shapes, and the area of the polygon, is 2(½ × 2 × 3) + (½ × 6 × 3) + (6 × 3) = 33 square units.

Try the free Mathway calculator and problem solver below to practice various math topics. Try the given examples, or type in your own problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.