Negative Numbers and Integers
Negative Numbers
You may have visited certain cities in winter, or seen some movies showing very cold weather in other places. Do you know that the temperatures in very cold weathers are often below zero? For example, the winter temperature in Harbin, a city in northern China, may be 16 degrees Celsius below zero.
Mathematically, we express this situation of ‘below zero’ using negative numbers. A negative number is shown by placing the ‘–’ sign in front the number. Thus, the above temperature in Harbin would be –16 °C, which is read as ‘negative sixteen degrees Celsius.’
Can you think of other situations where you would use negative numbers?
Integers
You have already learned whole numbers, which are 0, 1, 2, 3, 4, 5, … Now, you observe that numbers can also be negative when they are below zero.
Whole numbers consist of zero and positive integers, which are 1, 2, 3, 4, …
Whole numbers, together with negative integers, form the set of integers. Examples of integers include –12, –7, –1, 0, 3, 6, 29, etc.
Zero is considered as neither positive nor negative.
Number Line
Integers can be represented as points on a number line.
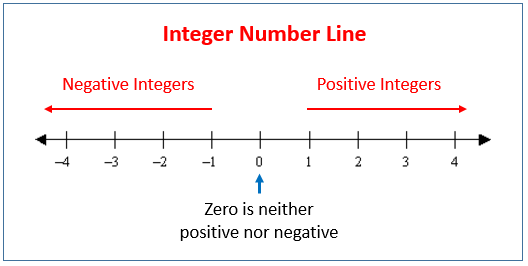
The arrows at the ends of the number line indicate continuity.
On a number line,
-
the space between any integer and the next has equal length
-
positive integers are placed to the right of zero. Positive integers may be written with the ‘+’ sign , i.e. +1, +2, +3, …, although we usually omit the ‘+’ sign and just write them as 1, 2, 3, … (Positive integers are also known as natural numbers.)
-
negative integers are placed to the left of zero. Negative integers must be written with the ‘–’ sign, i.e. –1, –2, –3, –4, …
-
each equal interval represents an equal number of units.
Absolute Value
The following figure explains Absolute Value. Scroll down the page for more examples and solutions.
Consider the numbers –3 and 3 on the number line. Note that they are at equal distance from 0 on the number line.
We say that –3 and 3 are opposites. Likewise, 2 is the opposite of –2, and –5 is opposite to 5. Every positive integer has an opposite by adding the ‘–’ sign.
The distance between 0 and any integer on the number line represents the absolute value of the integer. Thus, the absolute value of 3 is 3, and the absolute value of –3 is also 3. In other words, the absolute value for any integer is represented by the numeral only, disregarding the sign.
The notation |–6| means the absolute value of –6. Thus,
|–6| = 6, |5| = 5 and |–17| = 17
Comparing Integers
You have previously learned that 3 is larger than 2. We can write this as:
3 > 2, which we read as 3 is greater than 2, or
2 < 3, which is read as 2 is smaller than 3.
If you check the number line, you find that 3 is to the right of 2, showing that 3 is greater than 2, or 2 is to the left of 3, meaning that 2 is less than 3.
This works the same way for negative integers. Let us consider the integers
–1, –2, and –4. –4 is to the left of –2 or –1, so we can write
–4 < –2, and –4 < –1
Going the other way, –1 is to the right of –2 or –4, so,
–1 > –2, and –1 > –4
The following video will explain what are integers. Examples are given to explain the concept of positive and negative numbers.
The following video will explain the concept of absolute values and the number line
- Integers on a number line
- Opposite Integers
- Compare integers using the number line
Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.