Multiply 2-digit numbers by 2-digit numbers
Related Pages
Divide 2-digit numbers by 1-digit numbers
More Lessons for Grade 4 Math
Math Worksheets
These lessons help Grade 4 students learn how to multiply 2-digit numbers by 2-digit numbers. They include examples, solutions, videos, stories, and songs to help with multiplication skills.
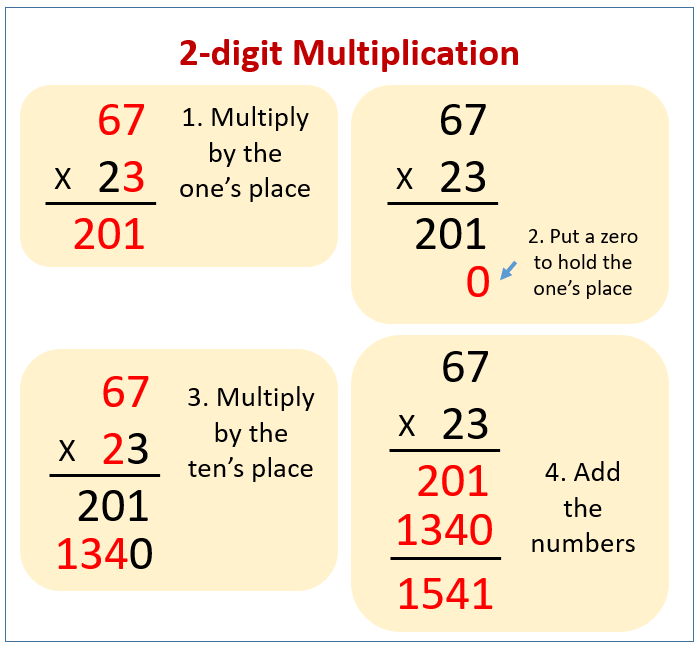
The following diagram shows how to multiply a 2-digit number by a 2-digit number. Scroll down the page for more examples and solutions on multiplying 2-digit numbers.
2-digit × 2-digit Multiplication Worksheets (printable & online)
Multiplying 2 digit number by another 2 digit number with regrouping
- Multiply by the one’s place.
- Put a zero to hold the ones’ place.
- Multiply by the number in the ten’s place.
- Add the numbers together.
Multiplication of two-digit numbers
Multiply 2 digits by 2 digits
Multiplying a 2-digit number by a 2-digit number
Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.