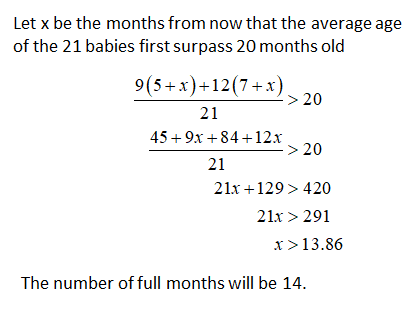Illustrative Mathematics Grade 7, Unit 6, Lesson 17: Modeling with Inequalities

Related Pages
Illustrative Math
Grade 7

Lesson 17: Modeling with Inequalities

Let’s look at solutions to inequalities.

Illustrative Math Unit 7.6, Lesson 17 (printable worksheets)

Lesson 17 Summary

We can represent and solve many real-world problems with inequalities. Whenever we write an inequality, it is important to decide what quantity we are representing with a variable. After we make that decision, we can connect the quantities in the situation to write an expression, and finally, the whole inequality.
As we are solving the inequality or equation to answer a question, it is important to keep the meaning of each quantity in mind. This helps us to decide if the final answer makes sense in the context of the situation.
For example: Han has 50 centimeters of wire and wants to make a square picture frame with a loop to hang it that uses 3 centimeters for the loop. This situation can be represented by 3 + 4s = 50, where s is the length of each side (if we want to use all the wire). We can also use 3 + 4s ≤ 50 if we want to allow for solutions that don’t use all the wire. In this case, any positive number that is less or equal to 11.75 cm is a solution to the inequality. Each solution represents a possible side length for the picture frame since Han can bend the wire at any point. In other situations, the variable may represent a quantity that increases by whole numbers, such as with numbers of magazines, loads of laundry, or students. In those cases, only whole-number solutions make sense.

Lesson 17.1 Possible Values

The stage manager of the school musical is trying to figure out how many sandwiches he can order with the $83 he collected from the cast and crew. Sandwiches cost $5.99 each, so he lets x represent the number of sandwiches he will order and writes 5.99x ≤ 83. He solves this to 2 decimal places, getting x ≤ 13.86.
Which of these are valid statements about this situation? (Select all that apply.)

1. He can call the sandwich shop and order exactly 13.86 sandwiches.
2. He can round up and order 14 sandwiches.
3. He can order 12 sandwiches.
4. He can order 9.5 sandwiches.
5. He can order 2 sandwiches.
6. He can order -4 sandwiches.

• See Video for Whole Lesson

Lesson 17.2 Elevator

A mover is loading an elevator with many identical 48-pound boxes.
The mover weighs 185 pounds. The elevator can carry at most 2000 pounds.

1. Write an inequality that says that the mover will not overload the elevator on a particular ride. Check your inequality with your partner.
2. Solve your inequality and explain what the solution means.
3. Graph the solution to your inequality on a number line.
4. If the mover asked, “How many boxes can I load on this elevator at a time?” what would you tell them?

Lesson 17.3 Giving Advice

Your teacher will give you either a problem card or a data card. Do not show or read your card to your partner.
If your teacher gives you the problem card:

1. Silently read your card and think about what information you need to answer the question.
2. Ask your partner for the specific information you need.
3. Explain to your partner how you are using the information to solve the problem.
4. Solve the problem and explain your reasoning to your partner.
   If your teacher gives you the data card:
   
5. Silently read the information on your card.
6. Ask your partner “What specific information do you need?” and wait for your partner to ask for information. Only give information that is on your card. (Do not figure out anything for your partner!)
7. Before telling your partner the information, ask, “Why do you need that information?”
8. After your partner solves the problem, ask them to explain their reasoning and listen to their explanation.
   Pause here so your teacher can review your work. Ask your teacher for a new set of cards and repeat the activity, trading roles with your partner.

Are you ready for more?

In a day care group, nine babies are five months old and 12 babies are seven months old. How many full months from now will the average age of the 21 babies first surpass 20 months old?

• Show Answer

  

Lesson 17 Practice Problems

1. 28 students travel on a field trip. They bring a van that can seat 12 students. Elena and Kiran’s teacher asks parents to drive cars that seat 3 children each to transport the rest of the students. Elena wonders if she should use the inequality 12 + 3n > 28 or 12 + 3n ≥ 28 to figure out how many cars are needed. Kiran doesn’t think it matters in this case. Do you agree with Kiran? Explain your reasoning.
2. a. In the cafeteria, there is one large 10-seat table and many smaller 4-seat tables. There are enough tables to fit 200 students. Write an inequality whose solution is the possible number of 4-seat tables in the cafeteria. b. 5 barrels catch rainwater in the schoolyard. Four barrels are the same size, and the fifth barrel holds 10 liters of water. Combined, the 5 barrels can hold at least 200 liters of water. Write an inequality whose solution is the possible size of each of the 4 barrels. c. How are these two problems similar? How are they different?
3. Solve each equation.
4. Select all the inequalities that have the same graph as x < 4.
5. A 200 pound person weighs 33 pounds on the moon. a. How much did the person’s weight decrease? b. By what percentage did the person’s weight decrease?

The Open Up Resources math curriculum is free to download from the Open Up Resources website and is also available from Illustrative Mathematics.

Try the free Mathway calculator and problem solver below to practice various math topics. Try the given examples, or type in your own problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.