Matrix Multiplication

Matrix multiplication might seem complicated at first, but it’s a systematic process.

How to multiply matrices

The most important rule is that you can only multiply two matrices if the number of columns in the first matrix is equal to the number of rows in the second matrix.

If matrix A is an m x n matrix (m rows and n columns) and matrix B is an n x p matrix (n rows and p columns), then you can multiply them, and the resulting matrix will be an m x p matrix.

A(2x3) can be multiplied by B(3x4). The result will be a 2x4 matrix. However, A(2x3) cannot be multiplied by B(4x3).

We will illustrate matrix multiplication or matrix product by the following example.

Example:

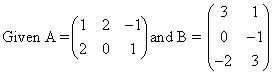
Find C = A × B

Solution:
Step 1: Multiply the elements in the first row of A with the corresponding elements in the first column of B. Add the products to get the element C₁₁.

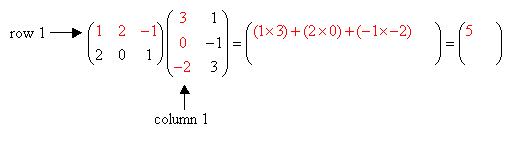
Showing Step 1 in detail:

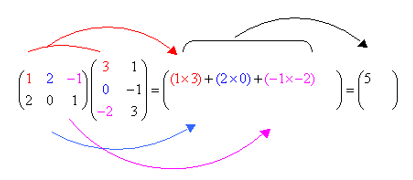
Step 2: Multiply the elements in the first row of A with the corresponding elements in the second column of B. Add the products to get the element C₁₂.

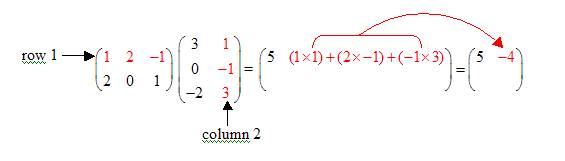
Step 3: Multiply the elements in the second row of A with the corresponding elements in the first column of B. Add the products to get the element C₂₁.

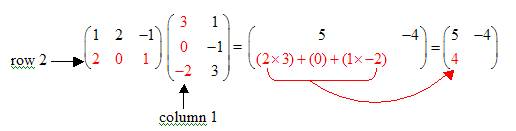
Step 4: Multiply the elements in the second row of A with the corresponding elements in the second column of B. Add the products to get the element C ₂₂.

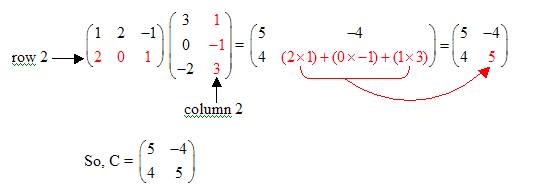
The following diagram shows another example of matrix multiplication.

Matrices that can or cannot be Multiplied

Not all matrices can be multiplied together.

For example, the product of A and B is not defined.

We cannot multiply A and B because there are 3 elements in the row to be multiplied with 2 elements in the column

This means that we can only multiply two matrices if the number of columns in the first matrix is equal to the number of rows in the second matrix.

An easy method to determine whether two matrices can be multiplied together would be to check the order of the matrices.

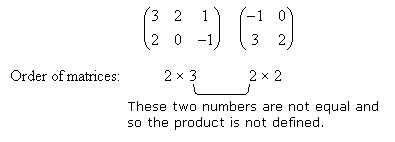
Can we multiply matrix A and matrix C?

We can also know the order of the product.

Working it out we can see that

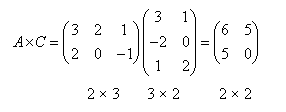
Checking the orders of the matrices will also help you to make sure that you multiplied the elements in the correct way.

Take note that matrix multiplication is not commutative that is generally

A × B ≠ B × A

Videos

Multiplying Matrices - Example 2
This video shows how to multiply a 2 × 3 matrix by a 3 × 1 matrix.

• Show Video Lesson

Multiplying Matrices - Example 3
This video shows how to multiply a 2 × 3 matrix by a 3 × 2 matrix.

• Show Video Lesson

Example of matrix multiplication

• Show Video Lesson

Matrix Multiplication
How to multiply matrices?

• Show Video Lesson

Try out our new and fun Fraction Concoction Game.

Add and subtract fractions to make exciting fraction concoctions following a recipe. There are four levels of difficulty: Easy, medium, hard and insane. Practice the basics of fraction addition and subtraction or challenge yourself with the insane level.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.