Describing Matrices (Rows and Columns)

A matrix is a rectangular array of numbers, symbols, or expressions, arranged in rows and columns.

The following diagram shows the rows and columns of a 3 by 2 matrix. Scroll down the page for more examples and solutions.

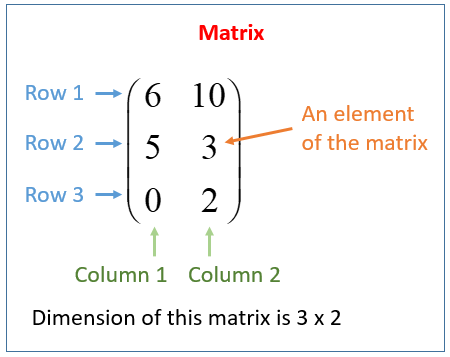
1. Dimensions (Order)
   The dimensions or order of a matrix gives the number of rows followed by the number of columns in a matrix. The order of a matrix with 3 rows and 2 columns is 3 × 2 or 3 by 2.

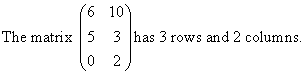
We usually denote a matrix by a capital letter.

C is a matrix of order 2 × 4 (read as ‘2 by 4’)

2. Elements In A Matrix
   Each number in the array is called an entry or an element of the matrix. When we need to read out the elements of a matrix, we read it out row by row.

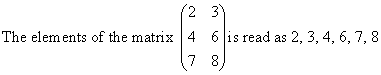
Each element is defined by its position in the matrix.

In a matrix A, an element in row i and column j is represented by a_ij.

Example:

a₁₁ (read as ‘a one one ’) = 2 (first row, first column)

a₁₂ (read as ‘a one two’) = 4 (first row, second column)

a₁₃ = 5, a₂₁ = 7, a₂₂ = 8, a₂₃ = 9

3. Equality:
   Two matrices are equal if and only if they have the same dimensions and their corresponding elements (entries in the same position) are equal.
   Learn about Equal Matrices
   

4. Addition:
   Condition: Matrix addition is only defined for matrices of the same dimensions.
   Process: To add two matrices, you add the corresponding elements.
   Properties:
   Commutative: A + B = B + A
   Associative: (A + B) + C = A + (B + C)
   Additive Identity: There exists a zero matrix (all elements are 0) such that A + 0 = A.
   Additive Inverse: For every matrix A, there exists a matrix -A such that A + (-A) = 0.
   Learn about Matrix Addition

5. Scalar Multiplication:
   Process: To multiply a matrix by a scalar (a single number), you multiply every element of the matrix by that scalar.
   Properties:
   Distributive: k(A + B) = kA + kB
   Distributive: (k + m)A = kA + mA
   Associative: (km)A = k(mA)
   Learn about Scalar Multiplication

6. Matrix Multiplication:
   Condition: To multiply two matrices A and B, the number of columns in A must be equal to the number of rows in B.
   Process: The element in the ith row and jth column of the product AB is found by taking the dot product of the ith row of A and the jth column of B.
   Properties:
   Associative: (AB)C = A(BC)
   Distributive: A(B + C) = AB + AC and (A + B)C = AC + BC
   Not Commutative (in general): AB ≠ BA (Matrix multiplication order matters)
   Multiplicative Identity: There exists an identity matrix I (a square matrix with 1s on the main diagonal and 0s elsewhere) such that AI = IA = A.
   Learn about Matrix Multiplication

7. Determinant (for Square Matrices):
   The determinant is a scalar value that can be computed from a square matrix. It has many important applications, including determining if a matrix is invertible.
   Denoted by |A| or det(A).
   Properties vary depending on the operation performed on the matrix.
   Learn about Determinant of a Matrix

8. Inverse (for Square Matrices):
   The inverse of a square matrix A (denoted A^-1) is a matrix such that AA^-1 = A^-1A = I, where I is the identity matrix.
   A matrix has an inverse if and only if its determinant is non-zero. Such a matrix is called invertible or non-singular. Otherwise, it is called singular.
   (AB)^-1 = B^-1A^-1
   Learn about the Inverse of a Matrix

9. Special Types of Matrices:
   Row Matrix (Row Vector): A matrix with only one row.
   Column Matrix (Column Vector): A matrix with only one column.
   Square Matrix: Number of rows = Number of columns.
   Diagonal Matrix: A square matrix where all non-diagonal elements are zero.
   Upper Triangular Matrix: A square matrix where all elements below the main diagonal are zero.
   Lower Triangular Matrix: A square matrix where all elements above the main diagonal are zero.
   Identity Matrix: A diagonal matrix where all diagonal elements are one.
   Zero Matrix (Null Matrix): A matrix where all elements are zero.
   Scalar Matrix: A diagonal matrix where all the diagonal elements are equal.
   Invertible Matrix (Non-singular Matrix): A square matrix that has an inverse
   Singular Matrix (Non-invertible Matrix): A square matrix that does not have an inverse. Its determinant is zero.
   Learn about Types of Matrices

Properties Of Matrices
The basics of a matrix. Looking at rows, columns, elements and dimension.
A matrix is a rectangular arrangement composed of row, columns and elements.
The dimensions of the matrix are determined by the number of rows and columns.

Example:
What are the dimensions of the matrix below? (in the video)

We can use a matrix to represent points, or a polygon. When we do this

• The x-coordinates are the first row.
• The y-coordinates are in the second row.
• Each point is a column.

Example:
What is the matrix for the following triangle? (in the video)

• Show Video Lesson

How to determine the dimension of a matrix and why it is important to be able to identify the dimensions of a matrix?

A matrix is a rectangular arrangement or array of numbers often called elements.

The size or dimensions m × n of a matrix identifies how many rows and columns a specific matrix has. The number of rows is m and the number of columns is n.

1. The dimension of a matrix must be known to identify a specific element in the matrix.
2. To add matrices, the dimensions must be the same.
3. To multiply matrices the number of columns in the first matrix must be the same number of rows in the second matrix.

• Show Video Lesson

How to state the dimensions of a matrix?

• Show Video Lesson

Introduction To Matrices

What a matrix is?
How to add and subtract matrices?

• Show Video Lesson

Check out our most popular games!
Fraction Concoction	Fact Family Game	Number Bond Garden
Online Addition Subtraction Game	Penguin Solitaire	Sawayama Solitaire
Ark Solitaire	Eldritch Invasion	Shenzhen Solitaire

Check out more Solitaire games here.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.