Locus Of A Moving Point

Related Pages
Loci In Geometry
Loci
More Geometry Lessons

The following diagrams give the locus of a point that satisfy some conditions. Scroll down the page for more examples and solutions.

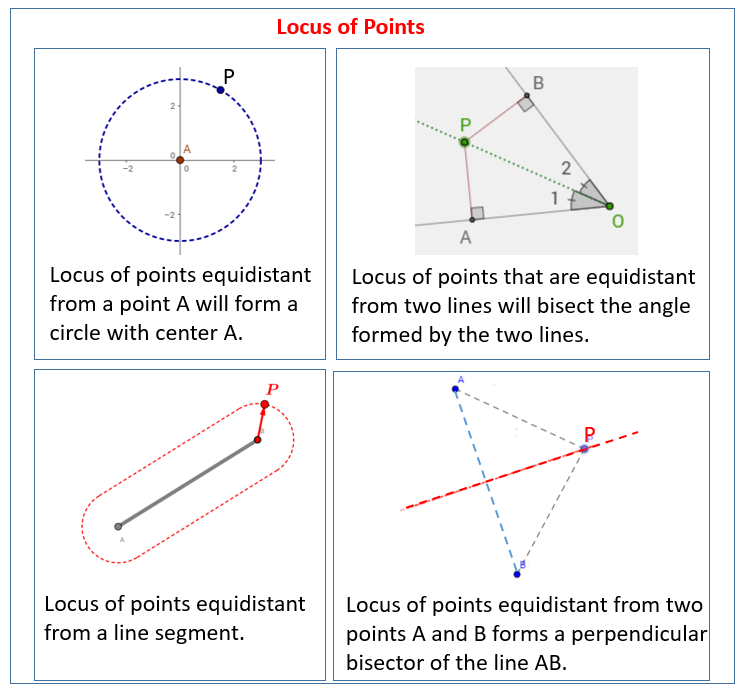
When a point moves in a plane according to some given conditions the path along which it moves is called a locus. (Plural of locus is loci.).

CONDITION 1:

A point P moves such that it is always m units from the point Q.

Locus formed: A circle with center Q and radius m.

Example:
Construct the locus of a point P at a constant distance of 2 cm from a fixed point Q.

Solution:
Construct a circle with center Q and radius 2 cm.

CONDITION 2:

A point P moves such that it is equidistant form two fixed points X and Y.

Locus formed: A perpendicular bisector of the line XY.

Example:
Construct the locus of point P moving equidistant from fixed points X and Y and XY = 6 cm.

Solution:
Construct a perpendicular bisector of the line XY.

CONDITION 3:

A point P moves so that it is always m units from a straight line AB.

Locus formed: A pair of parallel lines m units from AB.

Example:
Construct the locus of a point P that moves a constant distant of 2 cm from a straight line AB.

Solution:
Construct a pair of parallel lines 2 cm from AB.

CONDITION 4:

A point P moves so that it is always equidistant from two intersecting lines AB and CD.

Locus formed: Angle bisectors of angles between lines AB and CD.

Example:
The following figure shows two straight lines AB and CD intersecting at point O. Construct the locus of point P such that it is always equidistant from AB and CD.

Example:
Construct angles bisectors of angles between lines AB and CD.

Five Fundamental Locus Theorems And How To Use Them

Locus Theorem 1: The locus of points at a fixed distance, d, from the point, P is a circle with the given point P as its center and d as its radius.
Locus Theorem 2: The locus of the points at a fixed distance, d, from a line, l, is a pair of parallel lines d distance from l and on either side of l.
Locus Theorem 3: The locus of points equidistant from two points, P and Q, is the perpendicular bisector of the line segment determined by the two points.
Locus Theorem 4: The locus of points equidistant from two parallel lines, l₁ and l₂, is a line parallel to both l₁ and l₂ and midway between them.
Locus Theorem 5: The locus of points equidistant from two intersecting lines, l₁ and l₂, is a pair of bisectors that bisect the angles formed by l₁ and l₂.

Example 1:
A treasure map shows a treasure hidden in a park near a tree and a statue. The map indicates that the tree and the stature are 10 feet apart. The treasure is buried 7 feet from the base of the tree and also 5 feet from the base of the stature. How many places are possible locations for the treasure to be buried? Draw a diagram of the treasure map, and indicate with an X each possible location of the treasure.

Example 2:
The distance between the parallel line l and m is 12 units. Point A is on line l. How many points are equidistant from lines l and m and 8 units from point A.

Example 3:
Maria’s backyard has two trees that are 40 feet apart. She wants to place lampposts so that the the posts are 30 feet from both of the trees. Draw a sketch to show where the lampposts could be placed in relation to the trees. How many locations for the lampposts are possible?

• Show Video Lesson

Five Rules Of Locus Theorem Using Real World Examples

Locus is a set of points that satisfy a given condition.
There are five fundamental locus rules.
Rule 1: Given a point, the locus of points is a circle.
Rule 2: Given two points, the locus of points is a straight line midway between the two points.
Rule 3: Given a straight line, the locus of points is two parallel lines.
Rule 4: Given two parallel lines, the locus of points is a line midway between the two parallel lines.
Rule 5: Given two intersecting lines, the locus of points is a pair of lines that cut the intersecting lines in half.

• Show Video Lesson

Intersection Of Two Loci

Sometimes you may be required to determine the locus of a point that satisfies two or more conditions. We could do this by constructing the locus for each of the conditions and then determine where the two loci intersect.

Example:
Given the line AB and the point Q, find one or more points that are 3 cm from AB and 5 cm from Q.

Solution:
Construct a pair of parallel lines 3 cm from line AB. Draw a circle with center Q and radius 5 cm.

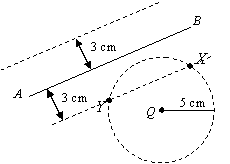
The points of intersections are indicated by points X and Y.

It means that the locus consists of the two points X and Y.

Example:
Given a square PQRS with sides 3 cm. Construct the locus of a point which is 2 cm from P and equidistant from PQ and PS. Mark the points as A and B.

Solution:
Construct a circle with center P and radius 2 cm. Since PQRS is a square the diagonal PR would be the angle bisector of the angle formed by the lines PQ and PS. The diagonal when extended intersects the circle at points A and B.

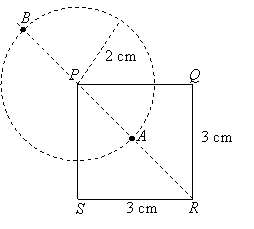
Note: A common mistake is to identify only one point when there could be another point which could be found by extending the construction lines or arcs; as in the above examples.

GCSE Maths Exam Questions - Loci, Locus And Intersecting Loci

Examples:

1. Draw
   (i) the locus of a point that moves so that it is always exactly 4 cm from the fixed point X and
   (ii) the locus of points less than 4 cm from the fixed point X.

2. Draw the locus of points no further than 3 cm from A and no further than 4 cm from B.

3. Draw the locus of a point exactly 3 cm away from straight line AB.

4. Draw
   (i) the locus of a point equidistant from the points X and Y.
   (ii) the locus of points closer to the point X than the point Y.
   (iii) the locus of points closer to X than Y but no less than 5 cm from X.

5. Draw the locus of points closer to the line AB than the line BC in the rectangle ABCD.

6. A dog is on a lead tethered to a post in the corner of a garden. The lead is 5 m long. A cat is free to roam all parts of the garden but is not allowed within 3 m of the house by its owner. Show the safe area that the cat can safely roam on the diagram below.

• Show Video Lesson

Try the free Mathway calculator and problem solver below to practice various math topics. Try the given examples, or type in your own problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.