Illustrative Mathematics Grade 8, Unit 3, Lesson 6: More Linear Relationships

Related Pages
Illustrative Math
Grade 8

Lesson 6: More Linear Relationships

Let’s explore some more relationships between two variables.

Illustrative Math Unit 8.3, Lesson 6 (printable worksheets)

Lesson 6 Summary

The following diagram shows how to match graphs to the real-world situations they represent by identifying the slope and the vertical intercept.

Lesson 6.1 Growing

Look for a growing pattern. Describe the pattern you see.

1. If your pattern continues growing in the same way, how many tiles of each color will be in the 4th and 5th diagram? The 10th diagram?
2. How many tiles of each color will be in the nth diagram? Be prepared to explain how your reasoning.

• See Video for Whole Lesson

Lesson 6.2 Slopes, Vertical Intercepts, and Graphs

Your teacher will give you 6 cards describing different situations and 6 cards with graphs.

1. Match each situation to a graph.
2. Pick one proportional relationship and one non-proportional relationship and answer the following questions about them. a. How can you find the slope from the graph? Explain or show your reasoning. b. Explain what the slope means in the situation. c. Find the point where the line crosses the vertical axis. What does that point tell you about the situation?

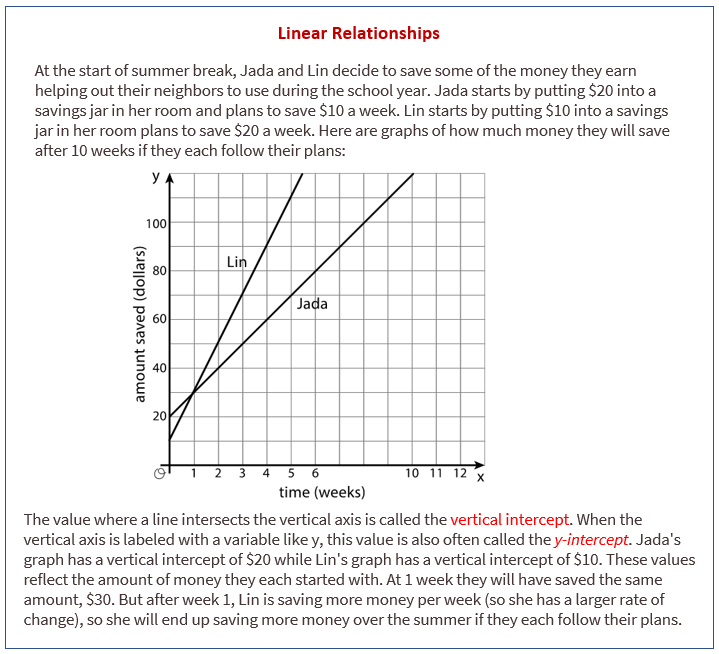
Lesson 6.3 Summer Reading

Lin has a summer reading assignment. After reading the first 30 pages of the book, she plans to read 40 pages each day until she finishes. Lin makes the graph shown here to track how many total pages she’ll read over the next few days.
After day 1, Lin reaches page 70, which matches the point (1,70) she made on her graph. After day 4, Lin reaches page 190, which does not match the point (4,160) she made on her graph. Lin is not sure what went wrong since she knows she followed her reading plan.

1. Sketch a line showing Lin’s original plan on the axes.
2. What does the vertical intercept mean in this situation? How do the vertical intercepts of the two lines compare?
3. What does the slope mean in this situation? How do the slopes of the two lines compare?

Are you ready for more?

Jada’s grandparents started a savings account for her in 2010. The table shows the amount in the account each year.
If this relationship is graphed with the year on the horizontal axis and the amount in dollars on the vertical axis, what is the vertical intercept? What does it mean in this context?

• Show Answers

  The vertical intercept is 600.
  It was the starting amount in the year 2010.

Lesson 6 Practice Problems

1. Explain what the slope and intercept mean in each situation.
   a. A graph represents the perimeter, y, in units, for an equilateral triangle with side length x units. The slope of the line is 3 and the y-intercept is 0. b. The amount of money, y, in a cash box after x tickets are purchased for carnival games. The slope of the line is 1/4 and the y-intercept is 8.
   c. The number of chapters read, y, after x days. The slope of the line is 5/4 and the y-intercept is 2.
   d. The graph shows the cost in dollars, y, of a muffin delivery and the number of muffins, x, ordered. The slope of the line is 2 and the y-intercept is 3.
2. The graph shows the relationship between the number of cups of flour and the number of cups of sugar in Lin’s favorite brownie recipe.
   The table shows the amounts of flour and sugar needed for Noah’s favorite brownie recipe.
   a. Noah and Lin buy a 12-cup bag of sugar and divide it evenly to make their recipes. If they each use all their sugar, how much flour do they each need?
   b. Noah and Lin buy a 10-cup bag of flour and divide it evenly to make their recipes. If they each use all their flour, how much sugar do they each need?
3. Customers at the gym pay a membership fee to join and then a fee for each class they attend. Here is a graph that represents the situation.
   a. What does the slope of the line shown by the points mean in this situation?
   b. What does the vertical intercept mean in this situation?

The Open Up Resources math curriculum is free to download from the Open Up Resources website and is also available from Illustrative Mathematics.

Try the free Mathway calculator and problem solver below to practice various math topics. Try the given examples, or type in your own problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.