

Solving Linear Inequalities
More Lessons for GRE Math
Math Worksheets
This lesson is part of a series of lessons for the quantitative reasoning section of the GRE revised General Test. In this lesson, we will learn how to solve linear inequalities.
Linear Inequalities
A mathematical statement that uses one of the following inequality signs is called an inequality.
< less than
> greater than
≤ less than or equal to
≥ greater than or equal to
Inequalities can involve variables and are similar to equations, except that the two sides are related by one
of the inequality signs instead of the equality sign used in equations.
For example, the inequality x + 2 ≤ 7
is a linear inequality in one variable, which states that “x + 2 is less than or equal to 7.”
To
solve an inequality means to find the set of all values of the variable that make the inequality true. This
set of values is also known as the solution set of an inequality. Two inequalities that have the same
solution set are called equivalent inequalities.
The procedure used to solve a linear inequality is similar to that used to solve a linear equation, which is
to simplify the inequality by isolating the variable on one side of the inequality, using the following two
rules.
• When the same constant is added to or subtracted from both sides of an inequality, the direction
of the inequality is preserved and the new inequality is equivalent to the original.
• When both sides of the inequality are multiplied or divided by the same nonzero constant, the
direction of the inequality is preserved if the constant is positive but the direction is reversed if
the constant is negative. In either case, the new inequality is equivalent to the original.
For example,
Solve the inequality 7 – x < 9
7 – x < 9
7 – x – 7 < 9 – 7
– x < 2
x > –2 (remember to reverse the symbol when multiplying by –1 )
For example,
Solve ![]()
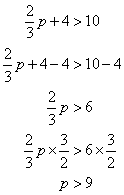
Try out our new and fun Fraction Concoction Game.
Add and subtract fractions to make exciting fraction concoctions following a recipe. There are four levels of difficulty: Easy, medium, hard and insane. Practice the basics of fraction addition and subtraction or challenge yourself with the insane level.



We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.