The Limits Of A Function
In these lessons, we will learn
- the definition of limits
- how to evaluate limits using direct substitution
- how to evaluate limits using factoring and canceling
- how to evaluate limits by combining fractions
- how to evaluate limits by expanding and simplifying
Related Pages
Introduction to Limits of Functions
Limits of Rational Functions
Calculate Limits using Different Techniques
Calculus Lessons
The following table gives the Existence of Limit Theorem and the Definition of Continuity. Scroll down the page for examples and solutions.
We have also included a limits calculator at the end of this lesson. This math tool will show you the steps to find the limits of a given function.
Definition Of Limits
We write
and say “the limit of f(x), as x approaches a, equals L”
if we can make the values of f(x) arbitrarily close to L by taking x to be sufficiently close
to a (on either side of a) but not equal to a.
This says that as x gets closer and closer to the number a (from either side of a) the values of f(x) get closer and closer to the number L In finding the limit of f(x) as x approaches, we never consider x = a. In fact, f(x) need not even be defined when x = a. The only thing that matters is how f(x) is defined near a.
What is a Limit?
Basic idea of Limits, informal definition of Limit, and what it means to calculate a limit.
In general, there are 3 ways to approach finding limits:
- Numerical Approach: t-table
- Graphical Approach: analyze the graph
- Analytical Approach: use algebra or calculus
What is the Limit Theorem?
As x approaches c, the limit of f(x) is L, if the limit from the left exists and the limit from the right exists and both limits are L.
Direct Substitution Property
If f is a polynomial or a rational function and a is the domain of f, then
Example:
Evaluate the following limits
Solution:
How to calculate the limit of a function using substitution?
Functions with Direct Substitution Property are called continuous at a. However, not all limits can be evaluated by direct substitution. The following are some other techniques that can be used.
Factoring And Canceling
Example:
Solution:
We can’t find the limit by substituting x = 1 because
is undefined.
Instead, we need to do some preliminary algebra. We factor the numerator as a difference of squares and then cancel out the common term (x – 1)
Therefore,
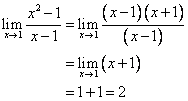
Note: In the above example, we were able to compute the limit by replacing the function
by
a simpler function g(x) = x + 1, with the same limit. This is valid because f(x) = g(x) except
when x = 1.
How to calculate a Limit By Factoring and Canceling?
How to calculate the limit of a function by using the factorization method?
If there are fractions within fractions, try to combine the fractions.
Example:
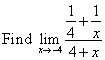
Solution:
We cannot use the substitution method because the numerator and denominator would be zero.
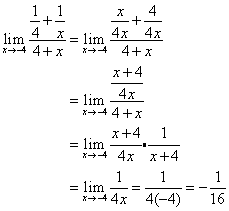
How to calculate a Limit by getting a Common Denominator?
If there is a square root, try to multiply by the conjugate.
Example:
Solution:
We cannot use the substitution method because the numerator and denominator would be zero.
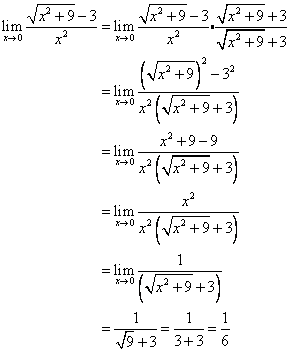
How to calculate a Limit by multiplying by a Conjugate?
Calculating a Limit by Expanding and Simplifying
A Limits Calculator or math tool that will show the steps to work out the limits of a given function. Use it to check your answers.
Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.