An Introduction to Functions
Related Pages
Inverse Functions
More Lessons for Intermediate Algebra
More Lessons for Algebra
Math Worksheets
A series of free, online Intermediate Algebra Lessons or Algebra II lessons.
Examples, solutions, videos, worksheets, and activities to help Algebra students.
In these lessons, we will learn
- how to define a function
- how to find the domain and range of a function
- how to use the Vertical Line Test
- how to define function notation
- how to calculate the composition of functions
Introduction to Functions
In mathematics, a relationship describes one quantity in terms of another. A function describes a relationship where each input has exactly one output.
An introduction to functions and how to identify whether or not a relationship is a function is very important building block since a lot of complex topics in upper-level math involve functions.
Vertical Line test
On a coordinate plane, the graph of a function y=f(x) passes the vertical line test: any vertical line drawn through the graph will intersect it at most once. This visually confirms that each input x has only one output y.
The following diagrams show the Vertical Line Test that can be used to test whether a given graph is a function. Scroll down the page for more examples and solutions on functions and how to use the Vertical Line Test.
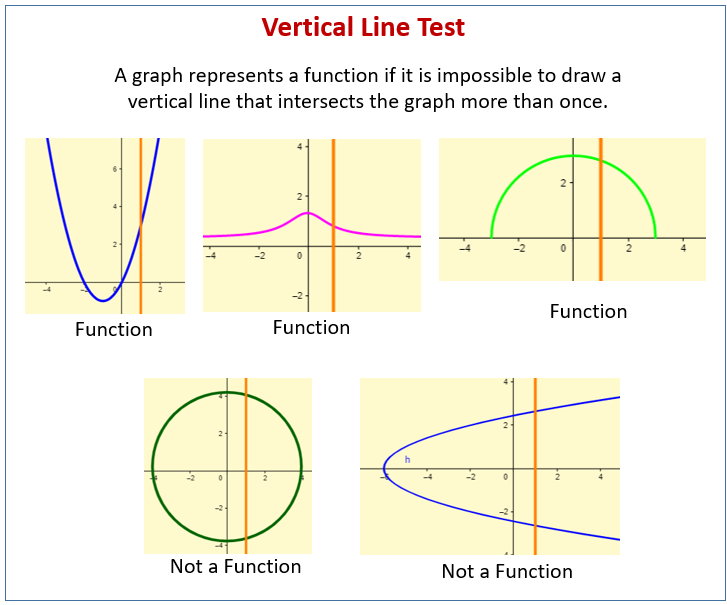
Domain and Range
An important part of understanding functions is understanding their domain and range. Domain and range are all the possible x-values and y-values of the function, and can often be described easily by looking at a graph. In order to grasp domain and range, students must understand how to determine if a relation is a function and interpreting graphs.
This video introduces the definition of a function, domain, and range.
This video shows how to graph a function and how to determine the domain and range of a function.
Vertical Line Test
Determine if a Relation is a Function
Determining Domain and Range
Function Notation
Throughout mathematics, we find function notation. Function notation is a way to write functions that is easy to read and understand. Functions have dependent and independent variables, and when we use function notation the independent variable is commonly x, and the dependent variable is F(x). In order to write a relation or equation using function notation, we first determine whether the relation is a function.
How to define function notation.
Function Notation - A basic description of function notation and a few examples involving function notation.
Composition of Functions
When we put two functions together, we have something called a composition of functions. For example, the expression g(f(x)) states that we should put the “f” function into the “g” function. To do this, we simply substitute the entire inner function into each of the variables in the outer function.
How to calculate the composition of functions.
Composition of Functions - Numerous examples are shown of how to compose functions
Check out our most popular games!
Fraction Concoction Game:
Master fractions in the lab: mix, add, and subtract beakers to create the perfect concoction!
Fact Family Game:
Complete fact families and master the link between addition & subtraction and multiplication & division.
Number Bond Garden:
Clear the board by matching number pairs that sum to ten in this garden-themed mental math puzzle.
Online Addition Subtraction Game:
Practice your addition and subtraction skills to help the penguin find its mummy.
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.