Illustrative Mathematics Unit 6.2, Lesson 1: Introducing Ratios and Ratio Language

Related Pages
Illustrative Math
Grade 6

Introducing Ratios And Ratio Language

Let’s describe two quantities at the same time.

Illustrative Math Unit 6.2, Lesson 1 (printable worksheets)

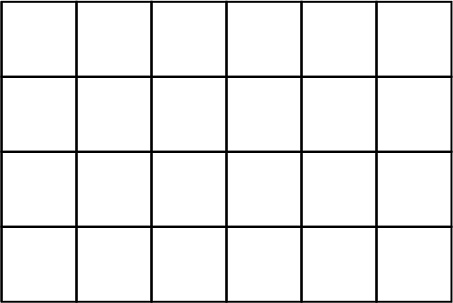
1.1 - What Kind and How Many?

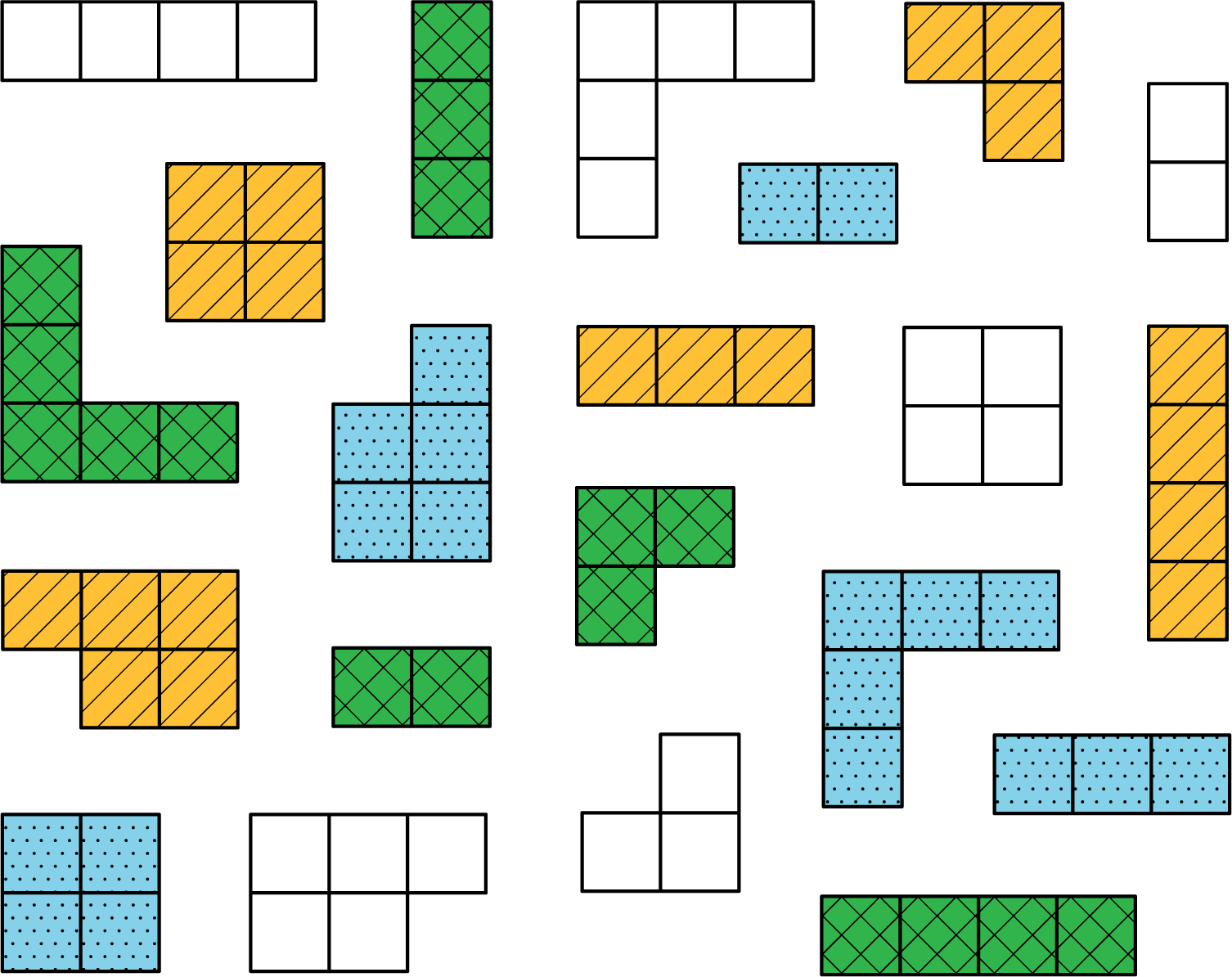
1. If you sorted this set by color (and pattern), how many groups would you have?
2. If you sorted this set by area, how many groups would you have?
3. Think of a third way you could sort these figures. What categories would you use? How many groups would you have?

• See Possible Answers
  1. There would be 4 groups: white (solid), green (cross-hatches), yellow (stripes) and blue (dots).
  2. There would be 4 groups: 2-squares, 3-squares, 4-squares, and 5-squares.
  3. One possible third way to sort these figures would be by shape. There are 7 distinct shapes (counting different rotations of a certain shape as 1 shape).
• See Video 1 for Whole Lesson
• See Video 2 for Whole Lesson

1.2 - The Teacher’s Collection

Your teacher will show you a collection of objects. Alternatively, consider the following collection:

• Show Collection

  

(1) Think of a way to sort your teacher’s collection into two or three categories. Record your categories in the top row of the table and the amounts in the second row.

category name
category amount

(2) Write at least two sentences that describe ratios in the collection. Remember, there are many ways to write a ratio as a sentence:

• The ratio of one category to another category is ________ to ________.
• The ratio of one category to another category is ________ : ________.
• There are _______ of one category for every _______ of another category.

(3) Make a visual display of your items that clearly shows one of your statements. Be prepared to share your display with the class.

• Definition Of Ratio

  A ratio is an association between two or more quantities. We can use this to compare quantities of objects between categories.

• See Possible Answers

  (1)
  

  category name	small	medium	large
  category amount	6	6	3

  
  

  (2) The ratio of small to large clips is 6 : 3.
  There are 6 medium clips for every 3 large clips

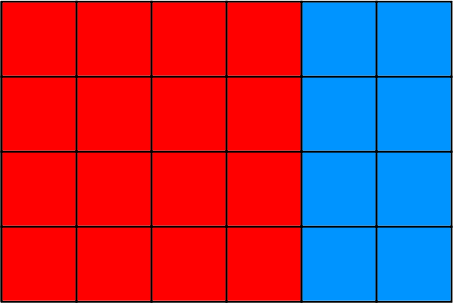
(1) Use two colors to shade the rectangle so there are 2 square units of one color for every 1 square unit of the other color.

• Show Grid for Coloring

  

(2) The rectangle you just colored has an area of 24 square units.
Draw a different shape that does not have an area of 24 square units, but that can also be shaded with two colors in a 2:1 ratio. Shade your new shape using two colors.

• See Possible Answers

  (1)
  
  There are 16 red squares for every 8 blue squares, which is the same as 2 red squares for every 1 blue square.

  (2)
  
  There are 8 red squares for every 4 blue squares, which is the same as 2 red squares for every 1 blue square.

Lesson 1 Summary

A ratio is an association between two or more quantities. There are many ways to describe a situation in terms of ratios. For example, look at this collection:

• Show Collection

  

Here are some correct ways to describe the collection:

• The ratio of squares to circles is 6 : 3.
• The ratio of circles to squares is 3 to 6.

Notice that the shapes can be arranged in equal groups, which allow us to describe the shapes using other numbers.

• Show Shapes

  

There are 2 squares for every 1 circle.
There is 1 circle for every 2 squares.

Glossary Terms

ratio: a ratio is an association between two or more quantities.

For example, the ratio 3:2 could describe a recipe that uses 3 cups of flour for every 2 eggs, or a boat that moves 3 meters every 2 seconds. One way to represent the ratio 3:2 is with a diagram that has 3 blue squares for every 2 green squares.

• Show Ratio

  

---

Practice Problems

(1) In a fruit basket there are 9 bananas, 4 apples, and 3 plums.

1. The ratio of bananas to apples is ________ : ________.
2. The ratio of plums to apples is ________ to ________.
3. For every ________ apples, there are ________ plums.
4. For every 3 bananas there is one ________.

• Answers
  1. The ratio of bananas to apples is 9 : 4.
  2. The ratio of plums to apples is 3 to 4.
  3. For every 4 apples, there are 3 plums.
  4. For every 3 bananas there is one plum.

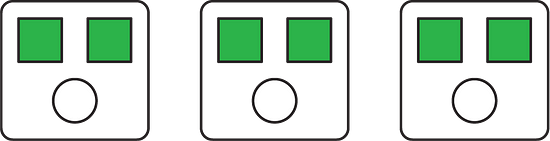
(2) Complete the sentences to describe this picture.

• Show Picture

  

1. The ratio of dogs to cats is _______.
2. For every _____ dogs, there are _____ cats.

• Answers
  1. The ratio of dogs to cats is 3:4.
  2. For every 3 dogs, there are 4 cats.

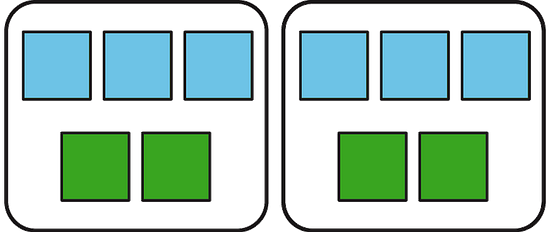
(3) Write two different sentences that use ratios to describe the number of eyes and legs in this picture.

• Show Picture

  

• Answers

  The ratio of eyes to legs is 4:8.

  For every 1 eye, there are 2 legs.

(4) Choose an appropriate unit of measurement for each quantity: cm, cm², or cm³.

1. area of a rectangle
2. volume of a prism
3. side of a square
4. area of a square
5. volume of a cube

• Answers
  1. area of a rectangle: cm² (2-dimensional)
  2. volume of a prism: cm³ (3-dimensional)
  3. side of a square: cm (1-dimensional)
  4. area of a square: cm²
  5. volume of a cube: cm³

(5) Find the volume and surface area of each prism.

a. Prism A: 3 cm by 3 cm by 3 cm

• Show Prism A

  

b. Prism B: 5 cm by 5 cm by 1 cm

• Show Prism B

  

c. Compare the volumes of the prisms and then their surface areas. Does the prism with the greater volume also have the greater surface area?

• Answers

  a. Volume = 3³ cm³ = 27 cm³
  Surface area = 6(3²) = 54 cm²

  b. Volume = 5 × 5 × 1 = 25 cm³
  Surface area = 2(5 × 5) + 4(5) = 70 cm²

  c. No. Prism A has a greater volume, but Prism B has a greater surface area.

(6) Which figure is a triangular prism? Select all that apply.

• Show Triangular Prism

  

• Answers

  A, C, and D are triangular prisms.

  Recall that prisms are polyhedra which consist of two congruent bases connected by rectangular faces, and that prisms are named after the shape of their bases. B is a pentagonal prism. E is a rectangular pyramid.

The Open Up Resources math curriculum is free to download from the Open Up Resources website and is also available from Illustrative Mathematics.

Try the free Mathway calculator and problem solver below to practice various math topics. Try the given examples, or type in your own problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.