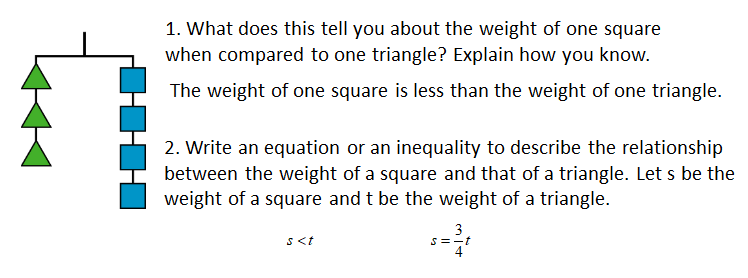Illustrative Mathematics Unit 6.7, Lesson 10: Interpreting Inequalities

Related Pages
Illustrative Math
Grade 6

Lesson 10: Interpreting Inequalities

Let’s examine what inequalities can tell us.

Illustrative Math Unit 6.7, Lesson 10 (printable worksheets)

Lesson 10 Summary

When we find the solutions to an inequality, we should think about its context carefully. A number may be a solution to an inequality outside of a context, but may not make sense when considered in context.

• Suppose a basketball player scored more than 11 points in a game, and we represent the number of points she scored, s, with the inequality s > 11. By looking only at s > 11, we can say that numbers such as 12, 14½, and 130.25 are all solutions to the inequality because they each make the inequality true.
  12 > 11
  14½ > 11
  130.25 > 11
  In a basketball game, however, it is only possible to score a whole number of points, so fractional and decimal scores are not possible. It is also highly unlikely that one person would score more than 130 points in a single game.
  In other words, the context of an inequality may limit its solutions.
  Here is another example:
  The solutions to r < 30 can include numbers such as 27¾, 18.5, 0, and -7. But if r represents the number of minutes of rain yesterday (and it did rain), then our solutions are limited to positive numbers. Zero or negative number of minutes would not make sense in this context.
  To show the upper and lower boundaries, we can write two inequalities:
  0 < r
  r < 30
  Inequalities can also represent comparison of two unknown numbers.
• Let’s say we knew that a puppy weighs more than a kitten, but we did not know the weight of either animal. We can represent the weight of the puppy, in pounds, with p and the weight of the kitten, in pounds, with k, and write this inequality:
  p > k
  

Lesson 10.1 True or False: Fractions and Decimals

Is each equation true or false? Be prepared to explain your reasoning.

1. 3(12 + 5) = (3 · 12) · (3 · 5)
2. 1/3 · 3/4 = 3/4 · 2/6
3. 2 · (1.5) · 12 = 4 · (0.75) · 6

• See Video for Whole Lesson

Scroll down the page for the solutions to the “Are you ready for more?” section.

Lesson 10.2 Basketball Game

Noah scored n points in a basketball game.

1. What does 15 < n mean in the context of the basketball game?
2. What does n < 25 mean in the context of the basketball game?
3. Draw two number lines to represent the solutions to the two inequalities.
4. Name a possible value for n that is a solution to both inequalities.
5. Name a possible value for n that is a solution to 15 < n, but not a solution to n < 25.
6. Can -8 be a solution to n in this context? Explain your reasoning.
   
   

Lesson 10.3 Unbalanced Hangers

1. Here is a diagram of an unbalanced hanger. An unbalanced hanger with the left side higher than the right side. On the left side, a pentagon. On the right side, a circle.
   Jada says that the weight of one circle is greater than the weight of one pentagon.
   a. Write an inequality to represent her statement. Let p be the weight of one pentagon and be the weight of one circle.
   b. A circle weighs 12 ounces. Use this information to write another inequality to represent the relationship of the weights. Then, describe what this inequality means in this context.
   
2. Here is another diagram of an unbalanced hanger.
   a. Write an inequality to represent the relationship of the weights. Let p be the weight of one pentagon and s be the weight of one square.
   b. One pentagon weighs 8 ounces. Use this information to write another inequality to represent the relationship of the weights. Then, describe what this inequality means in this context.
   c. Graph the solutions to this inequality on a number line.
   
3. Based on your work so far, can you tell the relationship between the weight of a square and the weight of a circle? If so, write an inequality to represent that relationship. If not, explain your reasoning.
   
4. This is another diagram of an unbalanced hanger.
   Andre writes the following inequality: c + p < s. Do you agree with his inequality? Explain your reasoning.
5. Jada looks at another diagram of an unbalanced hangar and writes: s +c > 2t, where t represents the weight of one triangle. Draw a sketch of the diagram.
   
   

Are you ready for more?

Here is a picture of a balanced hanger. It shows that the total weight of the three triangles is the same as the total weight of the four squares.

1. What does this tell you about the weight of one square when compared to one triangle? Explain how you know.
2. Write an equation or an inequality to describe the relationship between the weight of a square and that of a triangle. Let s be the weight of a square and t be the weight of a triangle.
   • Show Answers

     

   
   

Lesson 10 Practice Problems

1. There is a closed carton of eggs in Mai’s refrigerator. The carton contains e eggs and it can hold 12 eggs.
   a. What does the inequality e < 12 mean in this context?
   b. What does the inequality e > 0 mean in this context?
   c. What are some possible values of e that will make both e < 12 and e > 0 true?
   
2. Here is a diagram of an unbalanced hanger.
   a. Write an inequality to represent the relationship of the weights. Use s to represent the weight of the square in grams and c to represent the weight of the circle in grams.
   b. One red circle weighs 12 grams. Write an inequality to represent the weight of one blue square. c. Could 0 be a value of s? Explain your reasoning.
   
3. Tyler has more than $10. Elena has more money than Tyler. Mai has more money than Elena. Let t be the amount of money that Tyler has, let e be the amount of money that Elena has, and let m be the amount of money that Mai has. Select all statements that are true:
   A. t < m
   B. m > 10
   C. e > 10
   D. t > 10
   E. e > m
   F. t < e
   
4. a. Jada is taller than Diego. Diego is 54 inches tall (4 feet, 6 inches). Write an inequality that compares Jada’s height in inches, j, to Diego’s height.
   b. Jada is shorter than Elena. Elena is 5 feet tall. Write an inequality that compares Jada’s height in inches, j, to Elena’s height.
   
5. Which is greater, -9/20 or -0.5? Explain how you know. If you get stuck, consider plotting the numbers on a number line.
   
6. Select all the expressions that are equivalent to (½)³.
   A. ½ · ½ · ½
   B. 1/2³
   C. (⅓)²
   D. 1/6
   E. 1/8
   

The Open Up Resources math curriculum is free to download from the Open Up Resources website and is also available from Illustrative Mathematics.

Try the free Mathway calculator and problem solver below to practice various math topics. Try the given examples, or type in your own problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.