Illustrative Mathematics Grade 8, Unit 5, Lesson 1: Inputs and Outputs

Related Pages
Illustrative Math
Grade 8

Lesson 1: Inputs and Outputs

Let’s make some rules.

Illustrative Math Unit 8.5, Lesson 1 (printable worksheets)

Lesson 1 Summary

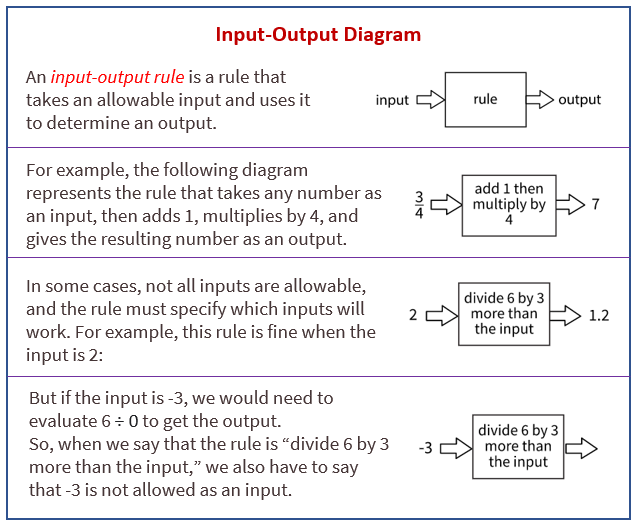
The following examples show how an input-output diagram represents a rule.

Lesson 1.1 Dividing by 0

Study the statements carefully.

• 12 ÷ 3 = 4 because 12 = 4 · 3
• 6 ÷ 0 = x because 6 = x · 0
  What value can be used in place of to create true statements? Explain your reasoning.

• See Video for Whole Lesson

Lesson 1.2 Guess My Rule

Try to figure out what’s happening in the “black box.”

Note: You must hit enter or return before you click GO.

Open Applet

Are you ready for more?

If you have a rule, you can apply it several times in a row and look for patterns. For example, if your rule was “add 1” and you started with the number 5, then by applying that rule over and over again you would get 6, then 7, then 8, etc., forming an obvious pattern.

Try this for the rules in this activity. That is, start with the number 5 and apply each of the rules a few times. Do you notice any patterns? What if you start with a different starting number?

Lesson 1.3 Making Tables

For each input-output rule, fill in the table with the outputs that go with a given input. Add two more input-output pairs to the table.

Are you ready for more?

Enter integers between -10 and 10. Try to figure out the rule. Open Applet

Lesson 1 Practice Problems

1. Given the rule:
   Complete the table for the function rule for the following input values:
   
2. Here is an input-output rule:
   Complete the table for the input-output rule:
3. Andre’s school orders some new supplies for the chemistry lab. The online store shows a pack of 10 test tubes costs $4 less than a set of nested beakers. In order to fully equip the lab, the school orders 12 sets of beakers and 8 packs of test tubes.
   a. Write an equation that shows the cost of a pack of test tubes, t, in terms of the cost of a set of beakers, b.
   b. The school office receives a bill for the supplies in the amount of $348. Write an equation with t and b that describes this situation.
   c. Since t is in terms of b from the first equation, this expression can be substituted into the second equation where t appears. Write an equation that shows this substitution.
   d. Solve the equation for b.
   e. How much did the school pay for a set of beakers? For a pack of test tubes?
4. Solve:
5. For what value of x do the expressions 2x + 3 and 3x - 6 have the same value?

The Open Up Resources math curriculum is free to download from the Open Up Resources website and is also available from Illustrative Mathematics.

Try the free Mathway calculator and problem solver below to practice various math topics. Try the given examples, or type in your own problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.