Surds (IGCSE Worked Examples)

Worked examples of problems on Surds as typically found in CIE IGCSE syllabus 0606 (and also CIE GCE O-Level syllabus 4037).

0606 W12 Paper 12 Question 6

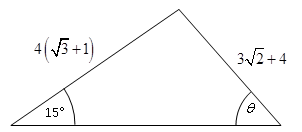
Using \(\sin 15^\circ = \frac{{\sqrt 2 }}{4}\left( {\sqrt 3 - 1} \right)\) and without using a calculator, find the value of \(\sin \theta\) in the form \(a + b\sqrt 2\), where \(a\) and \(b\) are integers.

Solution:
By Sine rule: \[\frac{{\sin \theta }}{{4\left( {\sqrt 3 + 1} \right)}} = \frac{{\sin 15^\circ }}{{3\sqrt 2 + 4}}\] \begin{align*} \sin \theta &= \sin 15^\circ \left( {\frac{{4\left( {\sqrt 3 + 1} \right)}}{{3\sqrt 2 + 4}}} \right)\\ &= \frac{{\sqrt 2 }}{4}\left( {\sqrt 3 - 1} \right)\left( {\frac{{4\left( {\sqrt 3 + 1} \right)}}{{3\sqrt 2 + 4}}} \right)\\ &= \frac{{\sqrt 2 \left( {\sqrt 3 - 1} \right)\left( {\sqrt 3 + 1} \right)}}{{3\sqrt 2 + 4}}\\ &= \frac{{\sqrt 2 \left( {3 - 1} \right)}}{{3\sqrt 2 + 4}}\\ &= \frac{{2\sqrt 2 }}{{3\sqrt 2 + 4}} \times \frac{{3\sqrt 2 - 4}}{{3\sqrt 2 - 4}}\\ &= \frac{{12 - 8\sqrt 2 }}{{18 - 16}}\\ &= 6 - 4\sqrt 2 \end{align*}