HCF & LCM

HCF and LCM using Factor Trees and Venn Diagrams
Finding the Highest Common Factor (HCF) and Lowest Common Multiple (LCM) of numbers is a fundamental concept in mathematics. Using factor trees and Venn diagrams provides a clear and visual way to understand these concepts, especially when dealing with larger numbers.

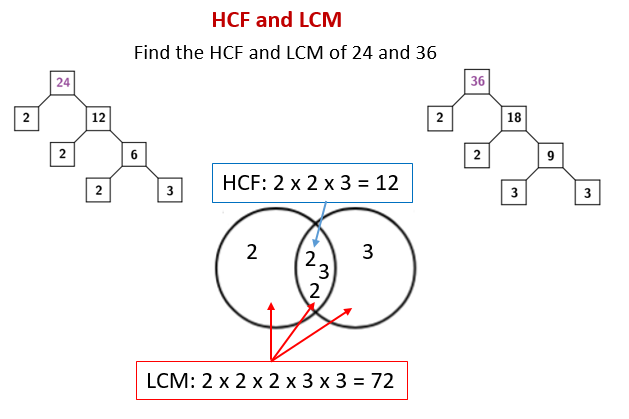
The following diagrams show how to find the HCF and LCM of 24 and 36 using Factor Trees and Venn Diagram. Scroll down the page for more examples.

 

Factors Worksheets
Practice your skills with the following worksheets:
Printable & Online Factors Worksheets

1. Prime Factorization (using Factor Trees)
The first step for both HCF and LCM is to break down each number into its prime factors. A factor tree is an excellent visual method for this. You break down the number into any two factors, then break down those factors, and so on, until all the “leaves” of the tree are prime numbers.

2. Organize Prime Factors into a Venn Diagram
Now, we’ll use a Venn diagram to visually represent the prime factors of each number. Draw two overlapping circles, one for each number.
Intersection (Overlap): Place all common prime factors in the overlapping section.
Unique Sections: Place any remaining (non-common) prime factors in the parts of the circles that do not overlap, in the circle corresponding to their original number.

3. Calculate HCF and LCM
a) Highest Common Factor (HCF)
The HCF is the product of all the prime factors in the intersection (the overlapping part) of the Venn diagram. These are the factors that are common to all the numbers.
b) Lowest Common Multiple (LCM)
The LCM is the product of all the prime factors found anywhere in the Venn diagram (including the unique sections and the common section), with each factor used only once from its position in the diagram.

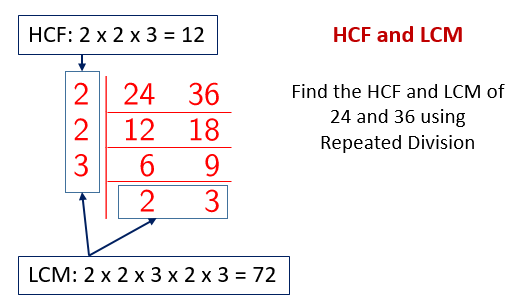
HCF and LCM using Repeated Division
For HCF using repeated division, you only divide by factors that are common to all the numbers.

For LCM using repeated division, you continue dividing until all numbers become 1. You divide by any prime factor that divides at least one of the numbers. If a number is not divisible by the prime factor, simply bring it down to the next row.

The following diagram shows how to find the HCF and LCM of 24 and 36 using Repeated Division.

Highest Common Factor, Lowest Common Multiple

GCSE Tutorial
Find HCF and LCM by listing, by prime factorization and by using Venn Diagrams.

Example:

1. Find the LCM and HCF of
   a) 8 and 12
   b) 6 and 16
   c) 24 and 42
   d) 72 and 84
   e) 80 and 36

• Show Video Lesson

How To Work Out HCF And LCM Using Short Division?

Example:
Find the HCF and LCM of 108 and 24.

• Show Video Lesson

How To Work Out HCF And LCM Using Prime Factorization?

Watch this GCSE maths revision lesson on Highest Common Factor (HCF) and Lowest Common Multiple (LCM).

Example:

1. Express 60 as the product of its prime factors.
2. Find the HCF of 24 and 36.
3. Find the LCM of 8 and 12.

• Show Video Lesson

How To Find The HCF And LCM Using Prime Factor Decomposition And Venn Diagrams?

Examples:

1. Work out the highest common factor (HCF) and lowest common multiple (LCM) of 48 and 60.
2. Work out the HCF and LCM of 140 and 210.

• Show Video Lesson

How To Use A Venn Diagram Method To Find LCM And HCF?

Find the LCM and HCF of 24 and 60.

• Show Video Lesson

How To Solve LCM And HCF (GCF) Word Problems?

Example:

1. William and Luis are in different physics class at Santa Rita. Luis’ teacher always gives exams with 30 questions while William’s teacher gives more frequent exams with only 24 questions. Luis’ teacher also assigns 3 projects per year. Even though the two classes have to take a different number of exams, their teachers have told them that both classes will get the same total number of exam questions each year.
   What is the minimum number of exam questions William’s or Luis’ class can expect to get in year?
2. Umaima just bought 1 package of 21 binders. She also bought 1 package of 30 pencils. She wants to use all the binders and pencils to create identical sets of office supplies for her classmates.
   What is the greatest number of identical sets Umaima can make using all the supplies?

• Show Video Lesson

How To Distinguish And Solve GCF (HCF) And LCM Word Problems?

Examples:

1. Sheila has 28 Skittle Bags and 36 Hershey Bars. If she wants to make goody bags with an equal amount of Skittles in each bag and an equal amount of Hershey Bars in each bag, what is the greatest number of bags she can make? How many Skittles will be in each bag? How many Hershey Bars will be in each bag?
2. Train A makes its stops in 45 minutes. Train B makes its stops in 60 minutes. How many minutes will pass before the two meet? In this time, how many loops will Train A make? How many loops will Train B make?

• Show Video Lesson

We also have a Highest Common Factor Calculator and a Least Common Multiple Calculator. Use them to check your answers.

The following Highest Common Factor Calculator will help you find the HCF of a list of numbers.

Greatest Common Factor Calculator
(Calculator Widget Copyright CalculatorSoup, LLC at www.calculatorsoup.com.)

The following Least Common Multiple Calculator will help you find the LCM of a list of numbers.

LCM Calculator - Least Common Multiple
(Calculator Widget Copyright CalculatorSoup, LLC at www.calculatorsoup.com.)

Try out our new and fun Fraction Concoction Game.

Add and subtract fractions to make exciting fraction concoctions following a recipe. There are four levels of difficulty: Easy, medium, hard and insane. Practice the basics of fraction addition and subtraction or challenge yourself with the insane level.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.