Greatest Common Factor (GCF)
Related Pages
Finding Greatest Common Factor
Least Common Multiple - LCM
More Arithmetic Lessons
Free Math Worksheets
In these lessons, we will learn how to find the GCF of two or more numbers
- by listing out the factors Click here
- by using the factor tree Click here
- by repetitive division (a faster method) Click here
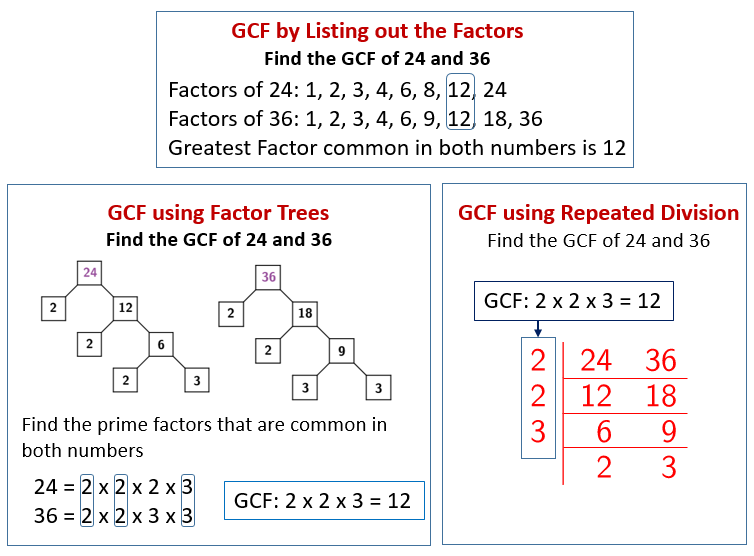
The following diagrams show how to find the GCF by listing out the factors, by using Factor Trees and by Repeated Division. Scroll down the page for more examples and solutions to find the greatest common factor (GCF).
Factors Worksheets
Practice your skills with the following Factors worksheets:
Printable & Online Factors Worksheets
How to find the GCF?
Listing Factors Method
This is often the easiest method for smaller numbers.
- List all the positive factors of each number.
- Identify the factors that appear in all of the lists (these are the common factors).
- The largest number among these common factors is the GCF.
Prime Factorization Method
This method is very reliable for any size of numbers, especially when numbers get larger.
- Find the prime factorization of each number. (You can use a factor tree).
- Identify all the prime factors that are common to all the numbers.
- Multiply these common prime factors together.
Ladder Method (or Upside-Down Division)
This method is a visual and organized way, especially good for finding the GCF of two or more numbers simultaneously.
- Write the numbers side by side.
- Find a common prime factor that divides all the numbers evenly. Write this prime factor to the left.
- Divide each number by that common prime factor and write the quotients (results) below the numbers.
- Repeat steps 2 and 3 with the new row of quotients until there are no more prime factors that divide all the numbers in the row.
- The GCF is the product of all the prime factors listed on the left side of the ladder.
Listing Out The Factors
In this method, we list out the factors of each number and then find the largest among the common factors.
Example:
Find the GCF of 48 and 60
Solution:
Factors of 48 are 1, 2, 3, 4, 6, 8, 12, 16, 24, 48
Factors of 60 are 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60
Common factors of 48 and 60 are 1,2,3,4,6,12.
The greatest factor is 12. So the GCF of 48 and 60 is 12.
How To Find The Gcf By Listing Out The Factors?
Example:
Find the GCF of 12 and 8, 25 and 20, 5 and 12, 6 and 12.
How To Find The Greatest Common Factor Of 16 And 20 By Listing Out The Factors?
Factor Trees
In this method, we use the factor tree to find the prime factors of each number. We then find the common prime factors and multiply them to get the greatest common factor.
How To Find The Greatest Common Factor Between Two Numbers By Using Factor Trees?
Example:
Find the GCF of 30 and 42.
Find The Greatest Common Factor By Using Prime Factorization (Factor Tree)
Example:
Find the GCF of 18 and 24, 72 and 90.
Greatest Common Factor Of 3 Numbers Using A Factor Tree
Here we find the Greatest Common Factor ( GCF ) of three numbers using a factor tree.
Example:
Find the GCF of 24, 32 and 72.
Repetitive Division
When the numbers are large, using the lists or factor tree to find the GCF can be slow and tedious. A faster method would be to use repetitive division to find the highest common factors.
Example:
Find the GCF of 48 and 60

The GCF of 48 and 60 is obtained by multiplying the numbers in the left column:
4 × 3 = 12
How to find the GCF of 24 and 36 using repetitive division?
Find The Greatest Common Factor (Gcf) For A Set Of Numbers Using The Upside Down Birthday Cake Method (Repetitive Division)
Example:
Find the GCF of 12 and 42, 32 and 96.
Try out our new and fun Fraction Concoction Game.
Add and subtract fractions to make exciting fraction concoctions following a recipe. There are four levels of difficulty: Easy, medium, hard and insane. Practice the basics of fraction addition and subtraction or challenge yourself with the insane level.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.