Greatest Common Divisor

Greatest Common Divisor

The Greatest Common Divisor (GCD), often also called the Highest Common Factor (HCF), of two or more non-zero integers is the largest positive integer that divides each of the integers without leaving a remainder.

The following diagrams show how to find the greatest common divisor (GCD). Scroll down the page for more examples and solutions on finding the greatest common divisor.

 

Factors Worksheets
Practice your skills with the following Factors worksheets:
Printable & Online Factors Worksheets

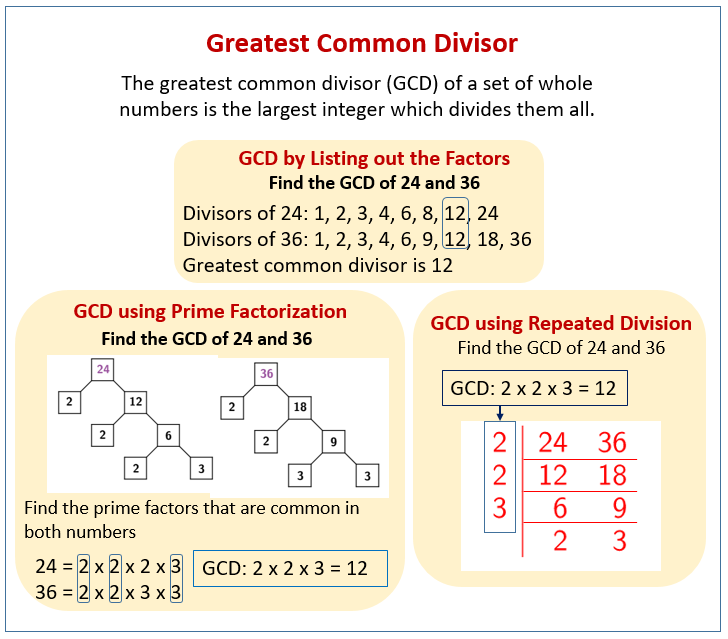
How to find the GCD?

Listing Divisors (Factors) Method
This method is straightforward for smaller numbers.
Steps:

1. List all the positive divisors (factors) of each number.
   
2. Identify the divisors that appear in all the lists (these are the common divisors).
   
3. The largest number among these common divisors is the GCD.
   

Prime Factorization Method
This method involves breaking down each number into its prime factors.
Steps:

1. Find the prime factorization of each number. (You can use a factor tree).
   
2. Identify and multiply all the prime factors that are common to all the numbers.
   

Use the repeated division or ladder method

1. Write the numbers for which you want to find the HCF in a horizontal row.
   
2. Find the smallest prime number that divides all the numbers evenly. Write this prime factor to the left of the numbers.
   
3. Divide each number by this common prime factor and write the quotients in a new row below the original numbers.
   
4. Continue steps 2 and 3 with the new row of quotients. Keep dividing by common prime factors until there are no more prime factors that divide all the numbers in the row.
   
5. The HCF is the product of all the prime factors listed on the left side of the ladder (the ones you divided by).

Greatest Common Divisors (GCDs)
Learn the definition of the “greatest common divisor” and solve three examples.

Examples:

1. Find gcd(12, 15)
2. Find gcd(9, 10)
3. Find gcd(9, 12, 21)

• Show Video Lesson

How to find the Greatest Common Divisor, using the factor tree method?

Examples:

1. Find the GCD of 72 and 8.
2. Find the GCD of 76 and 52.

• Show Video Lesson

Use “repeated division”, “double division” or the “ladder method” to find the GCF or GCD of two numbers

Example:
Find the GCD of 24 and 60

• Show Video Lesson

How to Find the Greatest Common Divisor by Using the Euclidean Algorithm?

Examples:
Find GCD(10, 45)
Find GCD(1701, 3768)

• Show Video Lesson

Try out our new and fun Fraction Concoction Game.

Add and subtract fractions to make exciting fraction concoctions following a recipe. There are four levels of difficulty: Easy, medium, hard and insane. Practice the basics of fraction addition and subtraction or challenge yourself with the insane level.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.