Graphing a Linear Equation

In this lesson, we will learn

• how to graph linear equations by plotting points. Click here
• how to graph linear equations by finding the x-intercept and y-intercept. Click here
• how to graph linear equations using the slope and y-intercept. Click here

The following diagrams show the different methods to graph a linear equation. Scroll down the page for more examples and solutions.

 

Printable & Online Coordinate Geometry Worksheets

Graph Linear Equations by Plotting Points

It takes only 2 points to draw a graph of a straight line. In other words, if we can find two points that satisfies the equation of the line, then the line can be accurately drawn. (You may plot more than two points to check)

1. Pick two or three different values for \(x\). Choose values that are easy to work with.
2. Substitute the x-values into the equation to find the corresponding y-values: For each chosen \(x\), solve the equation for \(y\). This will give you the coordinates of the points (\(x, y\)) that lie on the line.
3. Plot the ordered pairs (\(x, y)\) on the coordinate plane.
4. Using your straightedge, draw a straight line that passes through the plotted points. Extend the line to fill the graph.

Example:
Draw the line with equation y = 2x – 3

Solution:
Choose any value for x and substitute into the equation to get the corresponding value for y. If possible, try to choose values of x that will give whole numbers for y to make it easier to plot.
Step 1: Let x = 0
y = 2(0) – 3
y = – 3
Step 2: Let x = 2
y = 2(2) – 3
y = 1
Step 3: Plot the two points on the Cartesian
Step 4: Draw a straight line passing through the two points<br

 

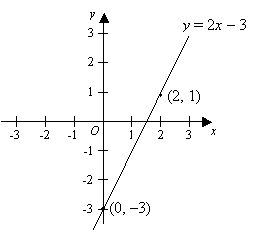
How to use a t-table to graph linear equations?
Example:
Graph the line for
a) y = 2x - 4
b) y = -1/2 x + 2

• Show Video Lesson

How to graph a linear equation by plotting points?
Example:
Graph the line
3x + 6y = 18

• Show Video Lesson

Graph Linear Equations by using X and Y Intercepts

If the linear equation is in the standard form \(Ax + By = C\), you can find the x and y-intercepts to graph the line.

1. Find the y-intercept: Set \(x = 0\) in the equation and solve for \(y\). This gives you the point \((0, y)\). Plot this point on the y-axis.
2. Find the x-intercept: Set \(y = 0\) in the equation and solve for \(x\). This gives you the point \((x, 0)\). Plot this point on the x-axis.
3. Draw the line: Using your straightedge, draw a straight line that passes through the x and y-intercepts. Extend the line to fill the graph.

How to find intercepts and use intercepts to graph linear equation?
Examples:

1. Find the intercepts of
   3x + y = 6
2. Graph x - y = 5
3. Find the intercepts and graph.
4. Plot the points and graph.

• Show Video Lesson

How to graph Linear Functions by finding the X-Intercept and Y-Intercept of the Function?
Examples:

1. Graph 2x + 4y = 12
2. Graph 3x - 2y = 8

• Show Video Lesson

Graph Linear Equations using Slope-Intercept

This is often the easiest and most intuitive method when the equation is already in or can be easily converted to the slope-intercept form:
\(y = mx + b\), where:
\(m\) is the slope (the rate of change, or rise over run: \(\frac{\text{rise}}{\text{run}}\)
\(b\) is the y-intercept (the point where the line crosses the y-axis, which is the point \((0, b)\)

How to graph an equation given in slope-intercept form?

1. Locate the value of \(b\) in the equation. This gives you the coordinates of the first point on your graph: \((0, b)\). Plot this point on the y-axis.
2. Locate the value of \(m\) in the equation. Remember that slope can be written as a fraction, \(m = \frac{\text{rise}}{\text{run}}\). If \(m\) is an integer, you can write it as \(\frac{m}{1}\).
3. Starting from the y-intercept you plotted in step 1, use the slope to find a second point.
   
4. Using your straightedge, draw a straight line that passes through the two points you’ve plotted. Extend the line to fill the graph.

What is the slope intercept formula and how to graph the equation?
Example:
Graph
a) y = 2x + 3
b) y = -2/3x - 2

• Show Video Lesson

How to graph a linear equation given in slope intercept form?
The equation y = mx + b is called the slope-intercept form of a line.
The equation represents a line where
m = slope
b = y-intercept (0, b)

Example:
Identify the slope and y-intercept. Graph.
a) y = -2/3 x + 1
b) y = 5x - 2
c) y = x
d) 3x - 2y = 8

• Show Video Lesson

Try out our new and fun Fraction Concoction Game.

Add and subtract fractions to make exciting fraction concoctions following a recipe. There are four levels of difficulty: Easy, medium, hard and insane. Practice the basics of fraction addition and subtraction or challenge yourself with the insane level.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.