Graphing Inequalities in Two Variables

Examples, solutions, videos, worksheets, and activities to help Algebra 1 students learn how to graph inequalities in two variables.

Graphing Inequalities with Two Variables
Just like equations, sometimes we have two variables in an inequality. Graphing inequalities with two variables involves shading a region above or below the line to indicate all the possible solutions to the inequality. When graphing inequalities with two variables, we use some of the same techniques used when graphing lines to find the border of our shaded region.

• The graph represents all of the solutions of the inequality and is a region in the plane.
  
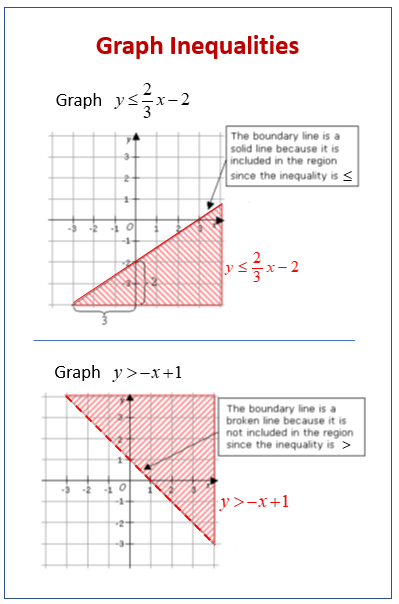
• The boundary of the region is the graph of the related equation (replace the inequality symbol with an equal to symbol “=”)
  • use a dotted line for < or > inequality
  • use a solid line for ≤ or ≥ inequality
  
• Use a test point to determine which side of the line contains the solutions.
  
• Shade the region of the plane that contains the solutions.

The following diagram shows some examples of graphing inequalities. Scroll down the page for more examples and solutions.

 

How to graph linear inequalities in two variables from Slope-Intercept and Standard forms?
How to use a test point to determine which region to shade?
Examples:
Graph the region of the plane that satisfies:

1. y < 1/2 x - 5
   
2. 2x - 4y ≤ 12
   
3. 3x + 5y > 30
   
4. y ≥ - 3/5 x + 4
   
5. y < 5
   
6. x ≥ - 2

• Show Step-by-step Solutions

Graphing Linear Inequalities Part 1
Basic graphing of linear inequalities in two variables.
Example:
3x + 2y ≤ 12

• Show Step-by-step Solutions

Graphing Linear Inequalities Part 2
Graphing a system of linear inequalities in two variables.
Example:
x + 2y ≤ 6
4x - y ≥ 8

• Show Step-by-step Solutions

Linear Inequalities in Two Variables
This video involves linear inequalities in two variables. Topics include: graphing the solution, determining if a line should be solid or dashed, determining which half-plane to shade.
Example:

1. Graph: 2x - 3y < 6
   
2. Graph: y ≥ 1/8 x + 2
   
3. Graph: y > 4x + 20

• Show Step-by-step Solutions

Try the free Mathway calculator and problem solver below to practice various math topics. Try the given examples, or type in your own problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.