Gradient of Straight Line Graphs

What is the gradient of a straight line?

The gradient (also known as the slope) of a straight line is a measure of its steepness and direction. It tells you how much the vertical distance changes for every unit change in the horizontal distance.

We commonly denote the gradient with the letter m.

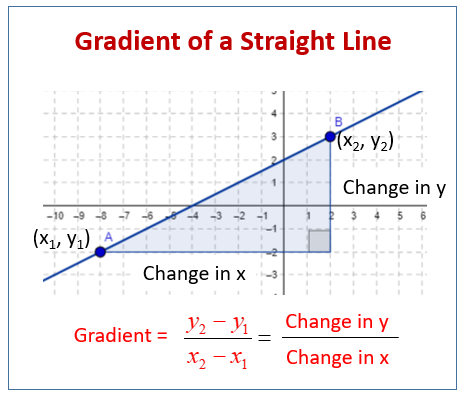
The following diagram shows how to find the gradient of a straight line graphs when given two points on the graph. Scroll down the page for more examples and solutions on finding the gradients of straight line graphs.


 

Coordinate Geometry Worksheets
Practice your skills with the following Coordinate Geometry worksheets:
Printable & Online Coordinate Geometry Worksheets

There are several ways to find the gradient of a straight line, depending on the information you have:

1. From Two Points on the Line
   Formula:
   Let the two points be (x₁, y₁) and (x₂, y₂).
   The gradient m is given by:
   \(m=\frac{\text{change in y}}{\text{change in x}}=\frac{y_2 - y_1}{x_2 - x_1}\)
   

2. From the Equation of the Line (Slope-Intercept Form)
   If the equation of the straight line is given in the slope-intercept form, y = mx + c, then the gradient is, m, the coefficient of x.
   

3. From a Graph
   If you have a graph of the straight line, you can count the grid lines to determine the “change in y” and “change in x” between any two clear points on the line.

Special Cases of Gradients:
A horizontal line has a gradient of 0.
The gradient of a vertical line is undefined.

Coordinate Geometry (Gradients of lines)
In this video, we learn how to

1. work out the gradient of a line given two points on the line.
   
2. select two points on a given line to work out the gradient.
   
3. use the gradient of a line and a known point on the line to work out the co-ordinates of a different point on the line.

• Show Step-by-step Solutions

Gradient between two points on straight line graph

• Show Step-by-step Solutions

Gradient of a line between two coordinates

• Show Step-by-step Solutions

Coordinate Geometry (Gradient of parallel and Perpendicular Lines)
In this question we will be dealing with straight line equations and how to find them given the gradient or two points on the line

• Show Step-by-step Solutions

Try out our new and fun Fraction Concoction Game.

Add and subtract fractions to make exciting fraction concoctions following a recipe. There are four levels of difficulty: Easy, medium, hard and insane. Practice the basics of fraction addition and subtraction or challenge yourself with the insane level.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.