Triangles for High School Geometry
Related Topics:
More Lessons for High School Geometry
More Lessons & Worksheets for Geometry
A series of free, online High School Geometry Video Lessons.
Videos, worksheets, and activities to help Geometry students.
In this lesson, we will learn
- exterior angles and remote interior angles of a triangle
- the triangle angle sum theorem
- the properties of an isosceles triangle
- the triangle inequality theorem
- the side inequalities and angle inequalities in a triangle
Remote Interior Angles
The following diagram shows that the sum of the two remote interior angles is equal to the exterior angles. Scroll down the page for more examples and solutions.
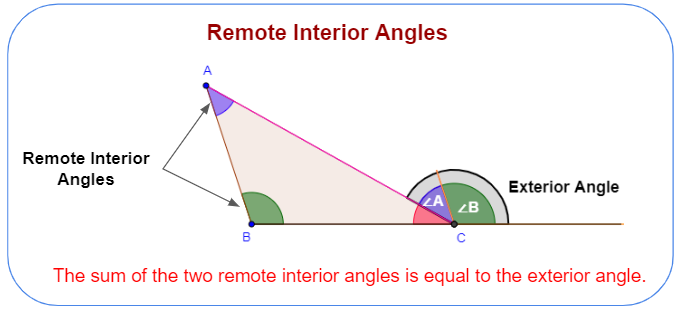
If one side of a triangle is extended beyond the vertex, an exterior angle is formed. This exterior angle is supplementary with its adjacent, linear angle. Since the angle sum in a triangle is also 180 degrees, the exterior angle must have a measure equal to the sum of the remaining angles, called the remote interior angles. How to define exterior angles and their remote interior angles and how to prove their properties
This video will define the interior and exterior angles of a triangle and then state several theorems involving the interior and exterior angles of a triangle.
Triangle Angle Sum
The sum of the three angles in any triangle sum to 180 degrees. The importance of this fact in Geometry cannot be emphasized enough. The triangle angle sum theorem is used in almost every missing angle problem, in the exterior angle theorem, and in the polygon angle sum formula.
How to apply and prove the triangle angle sum theorem.
How to use the angle sum of a triangle to find missing angles
Isosceles Triangle
Isosceles triangles have at least two congruent sides and at least two congruent angles. The congruent sides, called legs, form the vertex angle. The other two congruent angles are the base angles. Isosceles triangles are used in the regular polygon area formula and isosceles right triangles are known as 45-45-90 triangles.
How to define isosceles triangles, their components and how to determine their properties.
This video will demonstrate the names of the parts of an isosceles triangle, how to construct, and how to find angle measure.
Triangle Side Inequalities
The triangle inequality theorem states that the sum of any two sides of a triangle must be greater than the length of the third side. To find a range of values for the third side when given two lengths, write two inequalities: one inequality that assumes the larger value given is the longest side in the triangle and one inequality that assumes that the third side is the longest side in the triangle. Combine the two inequalities for the final answer.
How to determine the triangle side inequalities.
This video states and investigates the triangle inequality theorem.
Triangle Side and Angle Inequalities
In any triangle, the largest angle is opposite the largest side (the opposite side of an angle is the side that does not form the angle). The shortest angle is opposite the shortest side. Therefore, the angle measures can be used to list the size order of the sides. The converse is also true: the lengths of the sides can be used to order the relative size of the angles. Triangle side and angle inequalities are important when solving proofs.
How to determine the relationship between the side inequalities and angle inequalities in a triangle.
Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.