Geometry Common Core Regents Exam - June 2017
Related Topics:
More Lessons for the Regents High School Exam
More Lessons for Algebra
High School Math based on the topics required for the Regents Exam conducted by NYSED. The following are the worked solutions for the Geometry (Common Core) Regents High School Examination June 2017.
Geometry Common Core Regents New York State Exam - June 2017
The following are questions from the past paper Regents High School Geometry, June 2017 Exam (pdf). Scroll down the page for the step by step solutions.
Geometry - June 2017 Regents - Questions and solutions 1 - 12
- In the diagram below, ABC ≅ DEF.
Which sequence of transformations maps ABC onto DEF? - On the set of axes below, the vertices of PQR have coordinates P(6,7), Q(2,1), and R(1,3).
What is the area of PQR? - In right triangle ABC, m∠C = 90°. If cos B = 5/13, which function also equals 5/13?
- In the diagram below, mABC = 268°.
What is the number of degrees in the measure of ∠ABC? - Given MRO shown below, with trapezoid PTRO, MR = 9,MP = 2, and PO = 4.
What is the length of TR? - A line segment is dilated by a scale factor of 2 centered at a point not on the line segment. Which statement regarding the relationship between the given line segment and its image is true?
- Which figure always has exactly four lines of reflection that map the figure onto itself?
- In the diagram below of circle O, chord DF bisects chord BC at E.
If BC 12 and FE is 5 more than DE, then FE is - Kelly is completing a proof based on the figure below.
She was given that ∠A ≅ ∠EDF, and has already proven AB ≅ DE.
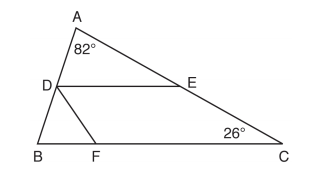
Which pair of corresponding parts and triangle congruency method would not prove ABC ≅ DEF? - In the diagram below, DE divides AB and AC proportionally, m∠C = 26°, m∠A = 82°, and DF bisects ∠BDE.
The measure of angle DFB is
11. Which set of statements would describe a parallelogram that can always be classified as a rhombus?
I. Diagonals are perpendicular bisectors of each other.
II. Diagonals bisect the angles from which they are drawn.
III. Diagonals form four congruent isosceles right triangles.
12. The equation of a circle is x2 + y2 - 12y + 20 = 0. What are the coordinates of the center and the length of the radius of the circle?
Geometry - June 2017 Regents - Questions and solutions 13 - 24
13. In the diagram of RST below, m∠T = 90°, RS = 65, and ST = 60.
What is the measure of ∠S, to the nearest degree?
14. Triangle A’B’C’ is the image of ABC after a dilation followed by a translation.
Which statement(s) would always be true with respect to this sequence of transformations?
15. Line segment RW has endpoints R(-4,5) and W(6,20). Point P is on RW such that RP:PW is 2:3. What are the coordinates of point P?
16. The pyramid shown below has a square base, a height of 7, and a volume of 84.
What is the length of the side of the base?
17. In the diagram below of triangle MNO, ∠M and ∠O are bisected by MS and OR, respectively. Segments MS and OR intersect at T, and m∠N = 40°.
If m∠TMR = 28°, the measure of angle OTS is
18. In the diagram below, right triangle ABC has legs whose lengths are 4 and 6.
What is the volume of the three-dimensional object formed by continuously rotating the right triangle around AB?
19. What is an equation of a line that is perpendicular to the line whose equation is 2y = 3x - 10 and passes through (6,1)?
20. In quadrilateral BLUE shown below, BE ≅ UL.
Which information would be sufficient to prove quadrilateral BLUE is a parallelogram?
21. A ladder 20 feet long leans against a building, forming an angle of 71° with the level ground. To the nearest foot, how high up the wall of the building does the ladder touch the building?
22. In the two distinct acute triangles ABC and DEF, ∠B ≅ ∠E. Triangles ABC and DEF are congruent when there is a sequence of rigid motions that maps
23. A fabricator is hired to make a 27-foot-long solid metal railing for computations. the stairs at the local library. The railing is modeled by the diagram below. The railing is 2.5 inches high and 2.5 inches wide and is comprised of a rectangular prism and a half-cylinder.
How much metal, to the nearest cubic inch, will the railing contain?
24. In the diagram below, AC 7.2 and CE 2.4.
Which statement is not sufficient to prove ABC ∼ EDC?
Geometry - June 2017 Regents - Questions and solutions Parts 2-4
25. Given: Trapezoid JKLM with JK || ML
Using a compass and straightedge, construct the altitude from vertex J to ML.
[Leave all construction marks.]
26. Determine and state, in terms of π, the area of a sector that intercepts a 40° arc of a circle with a radius of 4.5.
27. The diagram below shows two figures. Figure A is a right triangular prism and figure B is an oblique triangular prism. The base of figure A has a height of 5 and a length of 8 and the height of prism A is 14. The base of figure B has a height of 8 and a length of 5 and the height of prism B is 14.
Use Cavalieri’s Principle to explain why the volumes of these two triangular prisms are equal.
28. When volleyballs are purchased, they are not fully inflated. A partially inflated volleyball can be modeled by a sphere whose volume is approximately 180 in3. After being fully inflated, its volume is approximately 294 in3. To the nearest tenth of an inch, how much does the radius increase when the volleyball is fully inflated?
29. In right triangle ABC shown below, altitude CD is drawn to hypotenuse AB. Explain why ABC ∼ ACD.
30. Triangle ABC and triangle DEF are drawn below.
If AB ≅ DE, AC ≅ DF, and ∠A = ∠D, write a sequence of transformations that maps triangle ABC onto triangle DEF.
31. Line n is represented by the equation 3x + 4y = 20. Determine and state the equation of line p, the image of line n, after a dilation of scale factor 1/3 3 centered at the point (4,2).
[The use of the set of axes below is optional.]
Explain your answer.
32. Triangle ABC has vertices at A(-5,2), B(-4,7), and C(-2,7), and triangle DEF has vertices at D(3,2), E(2,7), and F(0,7). Graph and label ABC and DEF on the set of axes below.
Determine and state the single transformation where DEF is the image of ABC.
Use your transformation to explain why ABC ≅ DEF.
33. Given: RS and TV bisect each other at point X
TR and SV are drawn
Prove: TR || SV
34. A gas station has a cylindrical fueling tank that holds the gasoline for its pumps, as modeled below. The tank holds a maximum of 20,000 gallons of gasoline and has a length of 34.5 feet.
A metal pole is used to measure how much gas is in the tank. To the nearest tenth of a foot, how long does the pole need to be in order to reach the bottom of the tank and still extend one foot outside the tank? Justify your answer. [1 ft3 7.48 gallons]
35. Quadrilateral PQRS has vertices P(-2,3), Q(3,8), R(4,1), and S(-1,-4).
Prove that PQRS is a rhombus.
[The use of the set of axes on the next page is optional.]
Prove that PQRS is not a square.
[The use of the set of axes below is optional.]
36. Freda, who is training to use a radar system, detects an airplane flying at a constant speed and heading in a straight line to pass directly over her location. She sees the airplane at an angle of elevation of 15° and notes that it is maintaining a constant altitude of 6250 feet. One minute later, she sees the airplane at an angle of elevation of 52°. How far has the airplane traveled, to the nearest foot?
Determine and state the speed of the airplane, to the nearest mile per hour.
Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.