Geometry Common Core Regents Exam - January 2017
Related Topics:
More Lessons for the Regents High School Exam
More Lessons for Algebra
High School Math based on the topics required for the Regents Exam conducted by NYSED. The following are the worked solutions for the Geometry (Common Core) Regents High School Examination January 2017.
Geometry Common Core Regents New York State Exam - January 2017
The following are questions from the past paper Regents High School Geometry, January 2017 Exam (pdf). Scroll down the page for the step by step solutions.
Geometry - January 2017 Regents - Questions and solutions 1 - 12
-
Which equation represents the line that passes through the point (-2,2) and is parallel to y = 1/2 x + 8?
-
In the diagram below, ADE is the image of ABC after a reflection over the line AC followed by a dilation of scale factor AE/AC centered at point A.
-
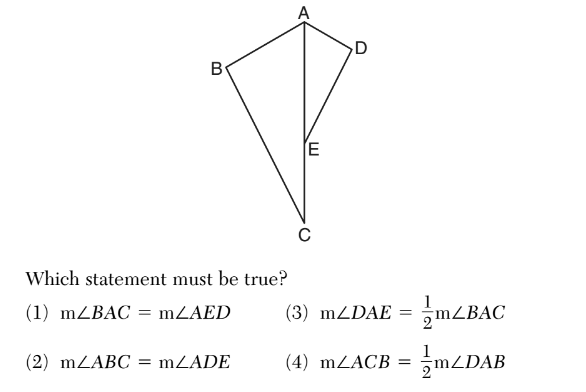
Given △ABC ≅ △DEF, which statement is not always true?
-
In the diagram below, DE, DF, and EF are midsegments of △ABC.
The perimeter of quadrilateral ADEF is equivalent to -
In the diagram below, if △ABE ≅ △CDF and is drawn, then it could be proven that quadrilateral ABCD is a
-
Under which transformation would △A’B’C’, the image of △ABC, not be congruent to △ABC?
-
The diagram below shows two similar triangles.
If tan θ = 3/7 , what is the value of x, to the nearest tenth? -
A farmer has 64 feet of fence to enclose a rectangular vegetable garden. Which dimensions would result in the biggest area for this garden?
-
The diagram shows rectangle ABCD, with diagonal BD.
-
Identify which sequence of transformations could map pentagon computations. ABCDE onto pentagon A"B"C"D"E", as shown below.
-
A solid metal prism has a rectangular base with sides of 4 inches and 6 inches, and a height of 4 inches. A hole in the shape of a cylinder, with a radius of 1 inch, is drilled through the entire length of the rectangular prism.
What is the approximate volume of the remaining solid, in cubic inches? -
Given the right triangle in the diagram below, what is the value of x, to the nearest foot?
Geometry - January 2017 Regents - Questions and solutions 13 - 24
13. On the graph below, point A(3,4) and with coordinates B(4,3) and C(2,1) are graphed.
What are the coordinates of B’ and C’ after BC undergoes a dilation centered at point A with a scale factor of 2?
14. In the diagram of right triangle ADE below, BC||DE. Which ratio is always equivalent to the sine of ∠A?
15. In circle O, secants ADB and AEC are drawn from external point A such that points D, B, E, and C are on circle O. If AD = 8, AE = 6, and EC is 12 more than BD, the length of BD is
16. A parallelogram is always a rectangle if
(1) the diagonals are congruent
(2) the diagonals bisect each other
(3) the diagonals intersect at right angles
(4) the opposite angles are congruent
17. Which rotation about its center will carry a regular decagon onto itself?
18. The equation of a circle is x2 + y2 - 6y + 1 = 0. What are the coordinates of the center and the length of the radius of this circle?
19. Parallelogram ABCD has coordinates A(0,7) and C(2,1). Which statement would prove that ABCD is a rhombus?
20. Point Q is on MN such that MQ:QN = 2:3. If M has coordinates (3,5) and N has coordinates (8,-5), the coordinates of Q are
21. In the diagram below of circle O, GO = 8 and m∠GOJ = 60°. What is the area, in terms of π, of the shaded region?
22. A circle whose center is the origin passes through the point (-5,12). Which point also lies on this circle?
23. A plane intersects a hexagonal prism. The plane is perpendicular to the base of the prism. Which two-dimensional figure is the cross section of the plane intersecting the prism?
24. A water cup in the shape of a cone has a height of 4 inches and a maximum diameter of 3 inches. What is the volume of the water in the cup, to the nearest tenth of a cubic inch, when the cup is filled to half its height?
Geometry - January 2017 Regents - Questions and solutions Parts 2-4
25. Using a compass and straightedge, construct the line of reflection over which triangle RST reflects onto triangle R"S"T". [Leave all construction marks.]
26. The graph below shows △ABC and its image, △A"B"C". Describe a sequence of rigid motions which would map △ABC onto △A"B"C".
27. When instructed to find the length of HJ in right triangle HJG, Alex wrote the equation sin 28° = HJ/20 while Marlene wrote cos 62° = HJ/20. Are both students’ equations correct? Explain why.
28. In the diagram below, tangent DA and secant DBC are drawn to circle O from external point D, such that AC ≅ BC. If mBC = 152°, determine and state m∠D.
29. In the diagram below, GI is parallel to NT, and IN intersects CT at A. Prove: △GIA ∼ △TNA
30. In the diagram below of isosceles triangle ABC, AB &song; CB and angle bisectors AD, BF, and CE are drawn and intersect at X.
If m∠BAC = 50°, find m∠AXC.
31. In square GEOM, the coordinates of G are (2,-2) and the coordinates of O are (-4,2). Determine and state the coordinates of vertices E and M. [The use of the set of axes below is optional.]
32. Triangle QRS is graphed on the set of axes below.
On the same set of axes, graph and label △Q’R’S’, the image of △QRS after a dilation with a scale factor of 3/2 centered at the origin.
33. Using a compass and straightedge, construct a regular hexagon inscribed in circle O below. Label it ABCDEF. [Leave all construction marks.]
If chords FB and FC are drawn, which type of triangle, according to its angles, would △FBC be?
Explain your answer.
34. A candle maker uses a mold to make candles like the one shown below.
The height of the candle is 13 cm and the circumference of the candle at its widest measure is 31.416 cm. Use modeling to approximate how much wax, to the nearest cubic centimeter, is needed to make this candle. Justify your answer.
35. In quadrilateral ABCD, AB ≅ CD, AB || CD, and BF and DE are perpendicular to diagonal AC at points F and E.
Prove: AE ≅ CF
36. New streetlights will be installed along a section of the highway. The posts for the streetlights will be 7.5 m tall and made of aluminum. The city can choose to buy the posts shaped like cylinders or the posts shaped like rectangular prisms. The cylindrical posts have a hollow core, with aluminum 2.5 cm thick, and an outer diameter of 53.4 cm. The rectangular-prism posts have a hollow core, with aluminum 2.5 cm thick, and a square base that measures 40 cm on each side. The density of aluminum is 2.7 g/cm3, and the cost of aluminum is $0.38 per kilogram. If all posts must be the same shape, which post design will cost the town less?
How much money will be saved per streetlight post with the less expensive design?
Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.