Geometry Common Core Regents Exam - August 2016
Related Topics:
More Lessons for the Regents High School Exam
More Lessons for Algebra
High School Math based on the topics required for the Regents Exam conducted by NYSED. The following are the worked solutions for the Geometry (Common Core) Regents High School Examination August 2016.
Geometry Common Core Regents New York State Exam - August 2016
The following are questions from the past paper Regents High School Geometry, August 2016 Exam (pdf). Scroll down the page for the step by step solutions.
Geometry - August 2016 Regents - Questions and solutions 1 - 12
1 In the diagram below, lines ℓ, m, n, and p intersect line r.
Which statement is true?
2 Which transformation would not always produce an image that would be congruent to the original figure?
3 If an equilateral triangle is continuously rotated around one of its medians, which 3-dimensional object is generated?
4 In the diagram below, m∠BDC = 100°, m∠A = 50°, and m∠DBC = 30°.
Which statement is true?
5 Which point shown in the graph below is the image of point P after a counterclockwise rotation of 90° about the origin?
6 In △ABC, where ∠C is a right angle, cos A = √21/5. What is sin B?
7 Quadrilateral ABCD with diagonals AC and BD is shown in the diagram below.
Which information is not enough to prove ABCD is a parallelogram?
8 An equilateral triangle has sides of length 20. To the nearest tenth, what is the height of the equilateral triangle?
9 Given: △AEC, △DEF, and FE ⊥ CE
What is a correct sequence of similarity transformations that shows AEC ∼ DEF?
10 In the diagram of right triangle ABC, CD intersects hypotenuse AB at D.
If AD = 4 and DB = 6, which length of AC makes CD ⊥ AB?
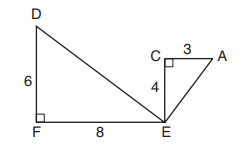
11 Segment CD is the perpendicular bisector of AB at E. Which pair of segments does not have to be congruent?
12 In triangle CHR, O is on HR, and D is on CR so that ∠H ≅ ∠RDO.
If RD = 4, RO = 6, and OH = 4, what is the length of CD?
Geometry - August 2016 Regents - Questions and solutions 13 - 24
13 The cross section of a regular pyramid contains the altitude of the pyramid. The shape of this cross section is a
14 The diagonals of rhombus TEAM intersect at P(2,1). If the equation of the line that contains diagonal TA is y = -x + 3, what is the equation of a line that contains diagonal EM?
15 The coordinates of vertices A and B of △ABC are A(3,4) and B(3,12). If the area of △ABC is 24 square units, what could be the coordinates of point C?
16 What are the coordinates of the center and the length of the radius of the circle represented by the equation
x2 + y2 - 4x + 8y + 11 = 0?
17 The density of the American white oak tree is 752 kilograms per cubic meter. If the trunk of an American white oak tree has a circumference of 4.5 meters and the height of the trunk is 8 meters, what is the approximate number of kilograms of the trunk?
18 Point P is on the directed line segment from point X(-6,-2) to point Y(6,7) and divides the segment in the ratio 1:5. What are the coordinates of point P?
19 In circle O, diameter AB, chord BC, and radius OC are drawn, and the measure of arc BC is 108°.
20 Tennis balls are sold in cylindrical cans with the balls stacked one on top of the other. A tennis ball has a diameter of 6.7 cm. To the nearest cubic centimeter, what is the minimum volume of the can that holds a stack of 4 tennis balls?
21 Line segment A’B’, whose endpoints are (4,-2) and (16,14), is the image of AB after a dilation of 1/2 centered at the origin. What is the length of AB?
22 Given: △ABE and △CBD shown in the diagram below with DB ≅ BE
Which statement is needed to prove ▵ABE ≅ ▵CBD using only SAS ≅ SAS?
23 In the diagram below, BC is the diameter of circle A.
Point D, which is unique from points B and C, is plotted on circle A. Which statement must always be true?
24 In the diagram below, ABCD is a parallelogram, AB is extended through B to E, and CE is drawn.
If CE ≅ BE and m∠D 112°, what is m∠E?
Geometry - August 2016 Regents - Questions and solutions 25 - 36
25 Lines AE and BD are tangent to circles O and P at A, E, B, and D, as shown in the diagram below. If AC:CE 5:3, and BD 56, determine and state the length of CD.
26 In the diagram below, △ABC has coordinates A(1,1), B(4,1), and C(4,5). Graph and label A"B"C", the image of △ABC after the translation five units to the right and two units up followed by the reflection over the line y = 0.
27 A regular hexagon is rotated in a counterclockwise direction about its center. Determine and state the minimum number of degrees in the rotation such that the hexagon will coincide with itself.
28 In the diagram of △ABC shown below, use a compass and straightedge to construct the median to AB. [Leave all construction marks.]
29 Triangle MNP is the image of triangle JKL after a 120° counterclockwise rotation about point Q. If the measure of angle L is 47° and the measure of angle N is 57°, determine the measure of angle M. Explain how you arrived at your answer.
30 A circle has a center at (1,–2) and radius of 4. Does the point (3.4,1.2) lie on the circle? Justify your answer.
31 In the diagram below, a window of a house is 15 feet above the ground. A ladder is placed against the house with its base at an angle of 75° with the ground. Determine and state the length of the ladder to the nearest tenth of a foot.
32 Using a compass and straightedge, construct and label △A’B’C’, the image of △ABC after a dilation with a scale factor of 2 and centered at B. [Leave all construction marks.]
33 The grid below shows △ABC and △DEF.
Let △A’B’C’ be the image of ABC after a rotation about point A. Determine and state the location of B’ if the location of point C’ is (8,–3). Explain your answer.
Is DEF congruent to A’B’C’? Explain your answer.
34 As modeled below, a movie is projected onto a large outdoor screen. The bottom of the 60-foot-tall screen is 12 feet off the ground. The projector sits on the ground at a horizontal distance of 75 feet from the screen.
Determine and state, to the nearest tenth of a degree, the measure of θ, the projection angle.
35 Given: Circle O, chords AB and CD intersect at E
Theorem: If two chords intersect in a circle, the product of the lengths of the segments of one chord is equal to the product of the lengths of the segments of the other chord.
Prove this theorem by proving AE · EB = CE · ED.
36 A snow cone consists of a paper cone completely filled with shaved ice and topped with a hemisphere of shaved ice, as shown in the diagram below. The inside diameter of both the cone and the hemisphere is 8.3 centimeters. The height of the cone is 10.2 centimeters.
The desired density of the shaved ice is 0.697 g/cm3, and the cost, per kilogram, of ice is $3.83. Determine and state the cost of the ice needed to make 50 snow cones.
Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.