SAT Practice Test 8, Section 5: Questions 16 - 20

This is for SAT in Jan 2016 or before.

The following are worked solutions for the questions in the math sections of the SAT Practice Tests found in the The Official SAT Study Guide Second Edition.

It would be best that you go through the SAT practice test questions in the Study Guide first and then look at the worked solutions for the questions that you might need assistance in. Due to copyright issues, we are not able to reproduce the questions, but we hope that the worked solutions will be helpful.

16. Correct answer: (A)

Given:
The graph of a quadratic function h whose maximum value is h(2)
h(a) = 0

To find:
The value of a

Solution:
If h(a) = 0, then x = a is where the graph intersects the x-axis.

The maximum value at h(2) means that the graph is symmetrical along the line x = 2

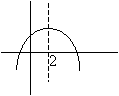
We can eliminate (B). If a = 0, then the graph must intersect the x-axis at x = 0. The given graph does not intersect the x-axis at x = 0. )

We can eliminate (C). If a = 2, then the graph must intersect the x-axis at x = 2. The given graph does not intersect the x-axis at x = 2.

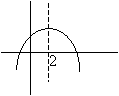
We can eliminate (D).If a = 3, then the graph must intersect the x-axis at x = 3.In order for the graph to intersect the x-axis at x = 3, the other intersection must be at x = 1 (to maintain the symmetry of the graph) and the graph would like that:

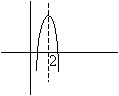
We can eliminate (E). If a = 4, then the graph must intersect the x-axis at x = 4. In order for the graph to intersect the x-axis at x = 4, the other intersection must be at x = 0 (to maintain the symmetry of the graph) and the graph would look like that:

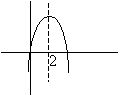
The only answer left is (A). If the graph intersects the x-axis at x = -1, the other intersection must be at x = 5 (to maintain the symmetry of the graph). A sketch the graph (as shown below) will indicate that it could be the given figure.

Answer: (A)

17. Correct answer: (D)

Given:
x² + kx + 7 = (x +1)(x + h)
k and h are constants

To find:
The value of k

Solution:
(x +1)(x + h)
= x² + hx + x + h
= x² + (h +1)x + h

Equating the 2 equations:
x² + (h +1)x + h = x² + kx + 7

We find that
h = 7
and k = h + 1 = 7 + 1 = 8

Answer: (D) 8

18. Correct answer: (A)

Given:
The figure
The legs of triangle ABC are parallel to the axes

To find:
Which of the following could be the length of the sides of triangle ABC

Solution:
Topic(s): Coordinate geometry, Pythagoras theorem

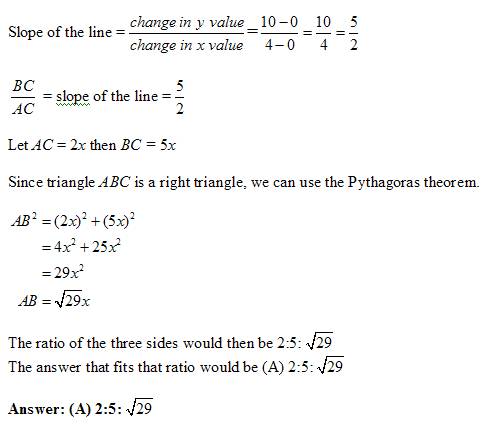
19. Correct answer: (E)

Given:
f(x) = 2x − 1

To find:
The value of t

Solution:
Topic(s): Isolate variable

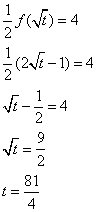
Answer: (E)

20. Correct answer: (E)

Given:
k is a positive integer

To find:
Which of the following represent an even integer that is twice the value of an odd integer

Solution:
Topic(s): Odd and even numbers

If k is an integer then 2k would be an even integer and

2k + 1 would be an odd integer.

Twice 2k + 1 = 2(2k + 1)= 4k + 2 would be an even integer

Answer: (E) 4k + 2