SAT Practice Test 2, Section 9: Questions 6 - 10

This is for SAT in Jan 2016 or before.

The following are worked solutions for the questions in the math sections of the SAT Practice Tests found in the The Official SAT Study Guide Second Edition.

It would be best that you go through the SAT practice test questions in the Study Guide first and then look at the worked solutions for the questions that you might need assistance in. Due to copyright issues, we are not able to reproduce the questions, but we hope that the worked solutions will be helpful.

Related Topics:

More SAT Math Help

More SAT Preparation

6. Correct answer: (C)

Given:
Three line segments meet at a point to form 3 angles

To find:
The angle x

Solution:
Topic(s): Angles

The sum of angles around a point = 360º.
2x + 4x + 3x = 360 ⇒ 9x = 360 ⇒ x = 40

Answer: (C) 40

7. Correct answer: (D)

Given:

y²=16
z > y
x, y and z are positive integers

To find:
x + z

Solution:
Topic(s): Exponents

You will need to know how to manipulate exponents. (Refer to the lesson on exponents if necessary ).

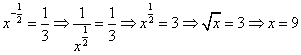
x + z = 9 + 4 = 13

Answer: (D) 13

8. Correct answer: (C)

Given:
A semicircle with center (4,0)

To find:
x-coordinates of two points on the semicircle whose y-coordinates are equal

Solution:
Topic(s): Coordinate geometry, Pythagoraean theorem

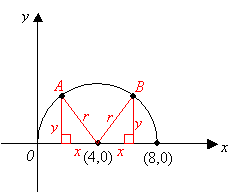
Let the two points at the semi-circle be A and B.

We can form two right triangles as shown in the diagram above.

Because A and B are on the semi-circle they are both the same distance r from the center (4,0). You are told that the two points A and B have the same y-coordinates.

Since the two corresponding sides of the two right triangles are equal (r and y) we can deduce from Pythagoras Theorem that the third side (x) should also be equal.

We now need to find, from the given answers, which pair is the same distance from (0,4).

(A) 1 and 6
4 – 1 = 3
6 – 4 = 2 (not the same)

(B) 1 and 8
4 – 1 = 3
8 – 4 = 4 (not the same)

(C) 2 and 6
4 – 2 = 2
6 – 4 = 2 (the same)

(D) 2 and 8
4 – 2 = 2
8 – 4 = 4 (not the same)

(E) 3 and 6
4 – 3 = 1
6 – 4 = 2 (not the same)

Answer: (C) 2 and 6

9. Correct answer: (B)

Given:
3 is the remainder when 2p + 7 is divided by 5
p is an integer

To find:
The value of p

Solution:
We are given that p is an integer and 3 is the remainder when 2p + 7 is divided by 5.
We can rewrite the question as 2p + 7 = 5n + 3 where n is an integer.

2p + 7 = 5n + 3
5n = 2p + 4

We now test out each of the answers to determine which value of p gives an integer value.

Answer: (B)

10. Correct answer: (B)

Given:
Everyone in the class is of a different height
Stacey is the 12 th tallest student and 12 th shortest student.

To find:
The number of students in the class

Solution:
Stacey is the 12 th tallest student and 12 th shortest student.

This means that if we order the students according to their heights, there would be 11 students before Stacey and 11 students after Stacey.

Altogether, there would then be 11 + 11 + 1 = 23 (don’t forget to count Stacey)

Answer: (B) 23