Illustrative Mathematics Unit 6.4, Lesson 13: Rectangles with Fractional Side Lengths

Related Pages
Illustrative Math
Grade 6

Lesson 13: Rectangles with Fractional Side Lengths

Let’s explore rectangles that have fractional measurements.

Illustrative Math Unit 6.4, Lesson 13 (printable worksheets)

Lesson 13 Summary

The following diagram shows how to use division and multiplication to solve problems involving areas of rectangles with fractional side lengths.

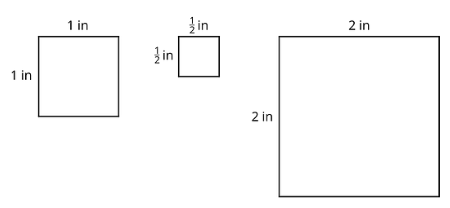
Lesson 13.1 Areas of Squares

• Show Squares

  

1. What do you notice about the areas of the squares? Write your observations.
   
2. Consider the statement: “A square with side lengths of ⅓ inch has an area of ⅓ square inches.” Do you agree or disagree with the statement? Explain or show your reasoning.

• See Video for Whole Lesson

Scroll down the page for the answer to the “Are you ready for more?” section.

Lesson 13.2 Areas of Squares and Rectangles

Use one piece of ¼-inch graph paper for the following.

1. Use a ruler to draw a square with side length of 1 inch on the graph paper. Inside the square, draw a square with side length of ¼ inch.
   a. How many squares with side length of ¼ inch can fit in a square with side length of 1 inch?
   b. What is the area of a square with side length of ¼ inch? Explain or show how you know.
   
2. Use a ruler to draw a rectangle that is 3½ inches by 2¼ inches on the graph paper. Write a division expression for each question and answer the question.
   a. How many ¼-inch segments are in a length of 3½ inches?
   b. How many ¼-inch segments are in a length of 2¼ inches?
   
3. Use your drawings to show that a rectangle that is 3½ inches by 2¼ inches has an area of 7 7/8 square inches.
   

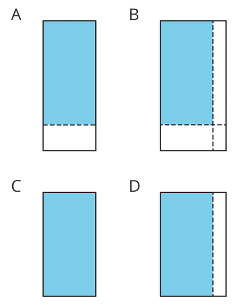
Lesson 13.3 Areas of Rectangles

Each of the following multiplication expressions represents the area of a rectangle.
2 · 4
2½ · 4
2 · 4¾
2½ · 4¾

1. All regions shaded in light blue have the same area. Match each diagram to the expression that you think represents its area. Be prepared to explain your reasoning.
   • Show Rectangles

     

2. Use the diagram that matches 2½ · 4¾ to show that the value of 2½ · 4¾ is 11 7/8.

Are you ready for more?

The following rectangles are composed of squares, and each rectangle is constructed using the previous rectangle. The side length of the first square is 1 unit.

• Show Rectangles

  

1. Draw the next four rectangles that are constructed in the same way. Then complete the table with the side lengths of the rectangle and the fraction of the longer side over the shorter side.

short side	long side	long side/short side
1
1
2
3

• Show Answer

  short side	long side	long side/short side
  1	1	1
  1	2	2
  2	3	3/2 = 1.5
  3	5	5/3 ≈ 1.67
  5	8	8/5 = 1.6
  8	13	13/8 = 1.625
  13	21	21/13 ≈ 1.615
  21	34	34/21 ≈ 1.619
  34	55	55/34 ≈ 1.617

2. Describe the values of the fraction of the longer side over the shorter side. What happens to the fraction as the pattern continues?

• Show Answer

  The fraction gets closer to 1.618. (This is known as the golden ratio 1.6180339887…)

Lesson 13.4 How Many Would it Take? (Part 2)

Noah would like to cover a rectangular tray with rectangular tiles. The tray has a width of 11½ inches and an area of 505/8 square inches.

1. Find the length of the tray in inches.
   
2. If the tiles are ¾ inch by 9/16 inch, how many would Noah need to cover the tray completely, without gaps or overlaps? Explain or show your reasoning.
   
3. Draw a diagram to show how Noah could lay the tiles. Your diagram should show how many tiles would be needed to cover the length and width of the tray, but does not need to show every tile.

Lesson 13 Practice Problems

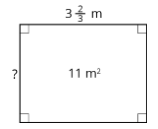
1. a. Find the unknown side length of the rectangle if its area is 11 m². Show your reasoning.
   • Show Rectangle

     

   b. Check your answer by multiplying it by the given side length (3⅔). Is the resulting product 11? If not, revisit your work for the first question.
   
2. A worker is tiling the floor of a rectangular room that is 12 feet by 15 feet. The tiles are square with side lengths 1⅓ feet. How many tiles are needed to cover the entire floor? Show your reasoning.
   
3. A television screen has length 16½ inches, width w inches, and area 462 square inches. Select all equations that represent the relationship of the side lengths and area of the television.
   A. w · 462 = 16½
   B. 16½ · w = 462
   C. 462 ÷ 16½ = w
   D. 462 ÷ w = 16½
   E. 16½ · 462 = w
   
4. The area of a rectangle is 17½ in² and its shorter side is 3½ in. Draw a diagram that shows this information. What is the length of the longer side?
   
5. A bookshelf is 42 inches long.
   a. How many books of length 1½ inches will fit on the bookshelf? Explain your reasoning.
   b. A bookcase has 5 of these bookshelves. How many feet of shelf space is there? Explain your reasoning.
   
6. Find the value of 5/32 ÷ 25/4. Show your reasoning.
7. How many groups of 1⅔ are in each of the following quantities?
   a. 1⅚
   b. 4⅓
   c. ⅚
   
8. It takes 1¼ minutes to fill a 3-gallon bucket of water with a hose. At this rate, how long does it take to fill a 50-gallon tub? If you get stuck, consider using the table.
   
   
   
   

The Open Up Resources math curriculum is free to download from the Open Up Resources website and is also available from Illustrative Mathematics.

Try the free Mathway calculator and problem solver below to practice various math topics. Try the given examples, or type in your own problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.