Illustrative Mathematics Unit 6.1, Lesson 9: Formula for the Area of a Triangle

Find out how to find the area of a triangle from its base and height. After trying the questions, click on the buttons to view answers and explanations in text or video.

Return to the list of Illustrative Math lessons

Formula for the Area of a Triangle
Let’s write and use a formula to find the area of a triangle.

Illustrative Math Unit 6.1, Lesson 9 (printable worksheets)

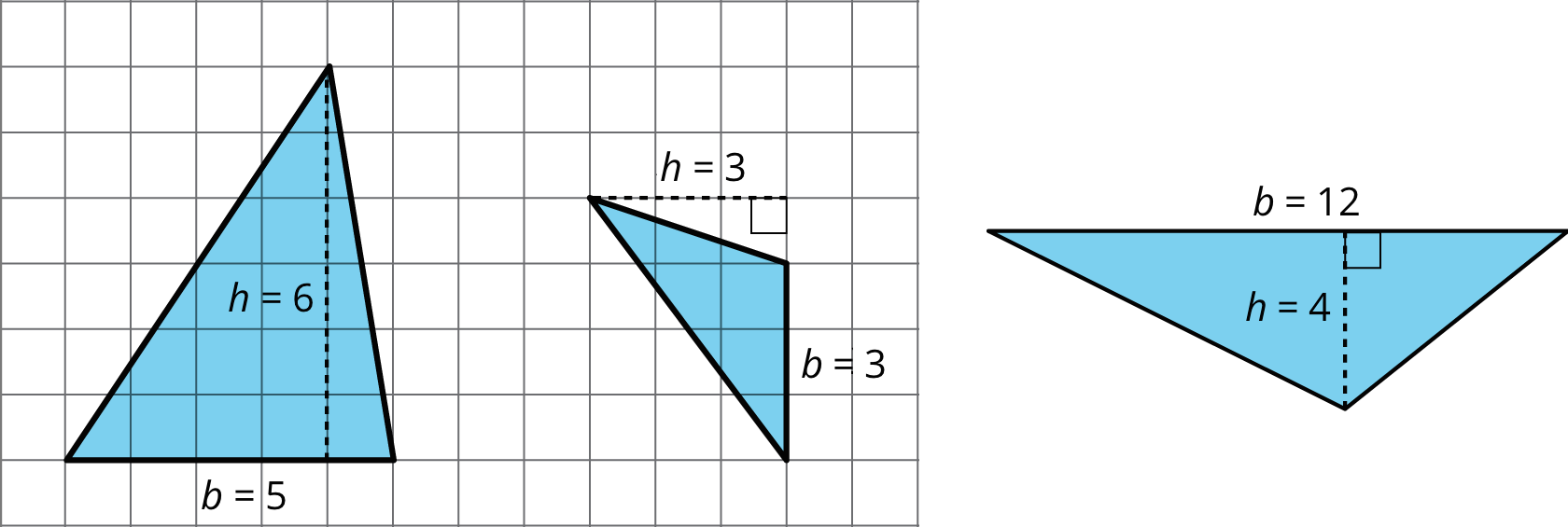
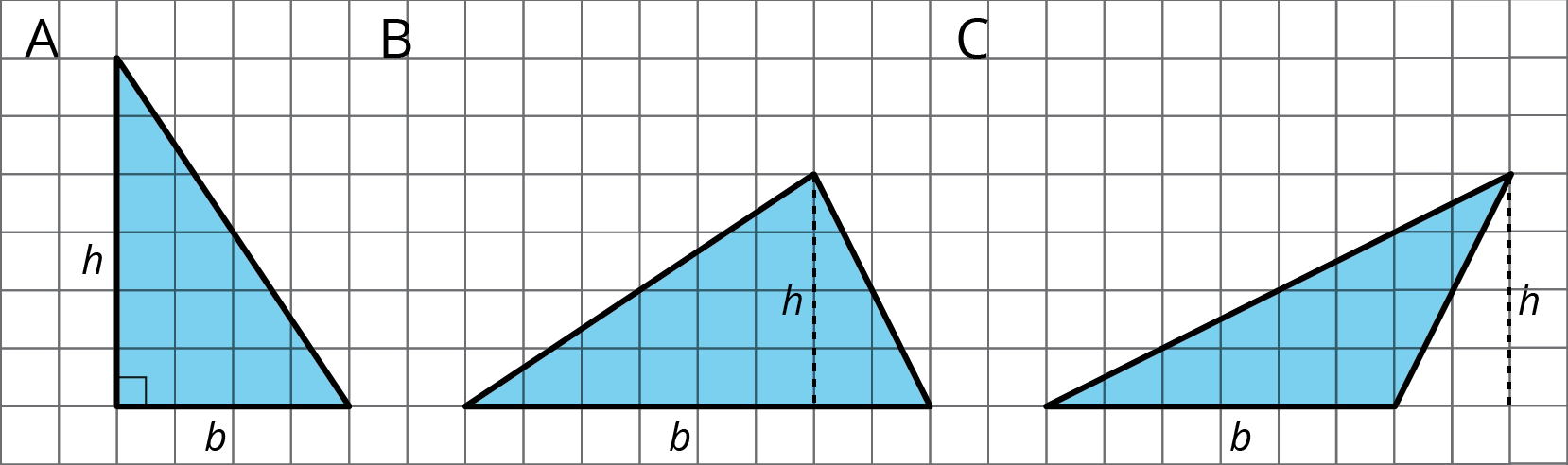
9.1 - Bases and Heights of a Triangle

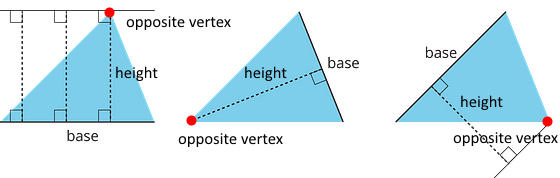
Study the examples and non-examples of bases and heights in a triangle. Answer the questions that follow.

These dashed segments represent heights of the triangle.

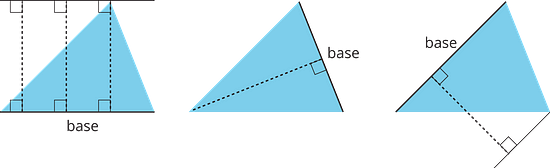
These dashed segments do not represent heights of the triangle.

Select all the statements that are true about bases and heights in a triangle. Give examples and counterexamples for your choices.

1. Any side of a triangle can be a base.
2. There is only one possible height.
3. A height is always one of the sides of a triangle.
4. A height that corresponds to a base must be drawn at an acute angle to the base.
5. A height that corresponds to a base must be drawn at a right angle to the base.
6. Once we choose a base, there is only one segment that represents the corresponding height.
7. A segment representing a height must go through a vertex.

How long should a segment that shows a height be?

• Show Answers

  1 is true. The three examples show the same triangle with different sides as the base.
  2 is false. The first example has three heights for a selected base.
  3 is false. The examples have heights that are not sides of the triangle.
  4 is false.
  5 is true. All the examples have heights drawn at right angles to their base, while some of the non-examples do not.
  6 is false. The first example has three heights for a selected base.
  7 is false. The third example has a height that does not pass through a vertex.

  The height should be a line segment perpendicular to the base, and should be as long as the distance between the base and the opposite vertex. The opposite vertex is the vertex that is not part of the base, as highlighted by the red dots below:
  

• See Video 1 for Whole Lesson

• See Video 2 for Whole Lesson

9.2 - Finding the Formula for Area of a Triangle

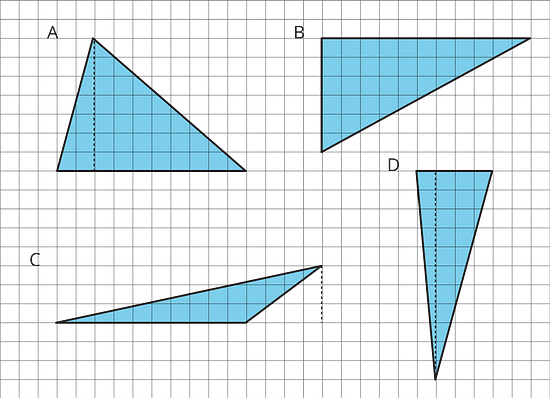
For each triangle, label a side that can be used as the base and a segment showing its corresponding height.
Record the measurements for the base and height in the table, and find the area of the triangle. (The side length of each square on the grid is 1 unit.)
In the last row, write an expression for the area of any triangle using b and h.

• Show Figures
  

triangle	base (units)	height (units)	area (sq units)
A
B
C
D
any triangle	b	h

• Hints

  Recall that in previous lessons, you could duplicate a triangle to form a parallelogram, and then divide the area of the parallelogram by half to find the area of a triangle. What is the formula for finding the area of a parallelogram? How might it change to become a formula for finding the area of a triangle?

• See Possible Answers
  

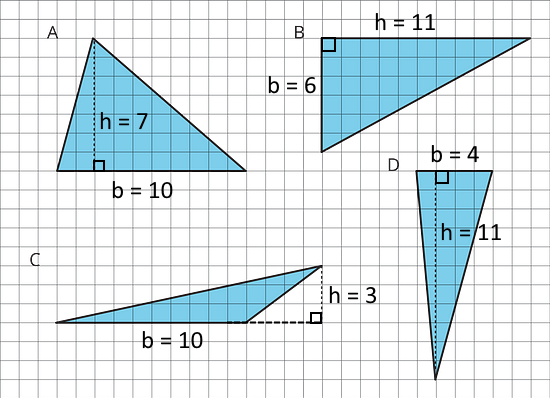
  triangle	base (units)	height (units)	area (sq units)
  A	10	7	35
  B	6	11	33
  C	10	3	15
  D	4	11	22
  any triangle	b	h	½ · b · h

  Other equivalent expressions, such as A = (b · h) ÷ 2, are also possible.

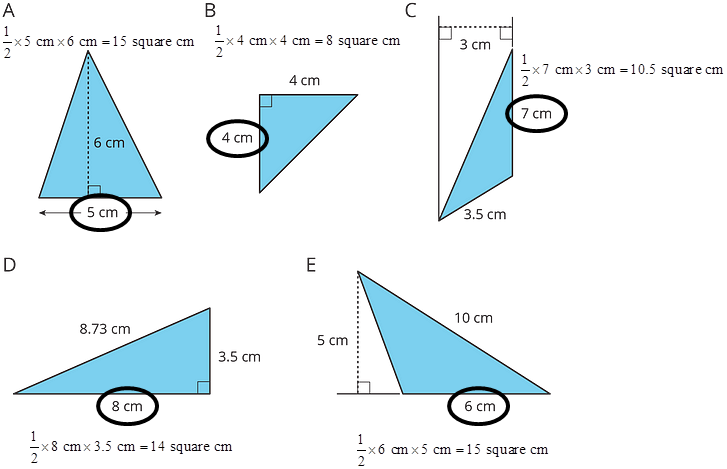
9.3 - Applying the Formula for Area of Triangles

For each triangle, circle a base measurement that you can use to find the area of the triangle. Then, find the area of any three triangles. Show your reasoning.

• Show Figures
  

• Hints

  Not all the measurements labeled on the diagrams are necessary for finding the area.

  The base of a triangle must be one of its sides.

  Choose a base in such a way that you know what the corresponding height is. Remember that the height must be perpendicular to the base you choose, and must show the distance between the base and the opposite vertex.

• See Possible Answers
  

  Note that the base of a triangle must be one of its sides.

  The measurements which are useful for finding the area of a triangle are a base and a corresponding height, which means the length of one side of the triangle and the length of a perpendicular segment between that side and the opposite vertex.

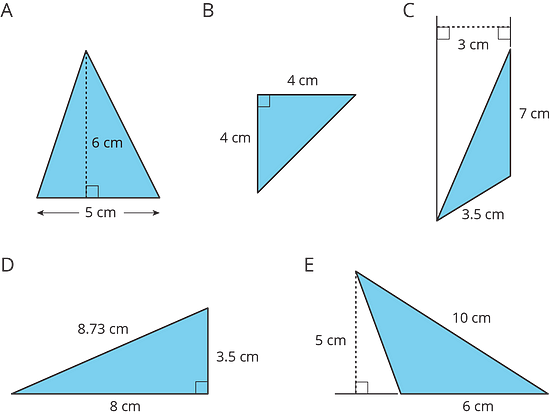
  In triangle C, the 3.5 cm side could be chosen as the base, but without a measurement for the corresponding height, it is not useful for finding the area.

  With right triangles like B or D, either of the two sides that form the right angle could be the base or the height. In non-right triangles—like A, C, and E—the height segment is not a side of the triangle; a different line segment has to be drawn.

  The formula for finding the area of a triangle is ½ · b · h.

  A: ½ × 5 cm × 6 cm = 15 square cm
  B: ½ × 4 cm × 4 cm = 8 square cm
  C: ½ × 7 cm × 3 cm = 10.5 square cm
  D: ½ × 8 cm × 3.5 cm = 14 square cm
  E: ½ × 6 cm × 5 cm = 15 square cm

Lesson 9 Summary

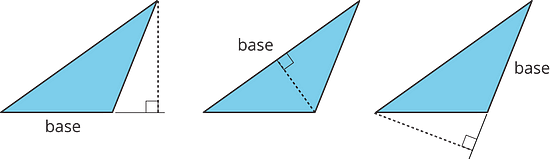
We can choose any of the three sides of a triangle to call the base. The term “base” refers to both the side and its length (the measurement).
The corresponding height is the length of a perpendicular segment from the base to the vertex opposite of it. The opposite vertex is the vertex that is not an endpoint of the base.

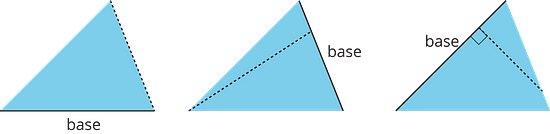
Here are three pairs of bases and heights for the same triangle. The dashed segments in the diagrams represent heights.

• Show Figures
  

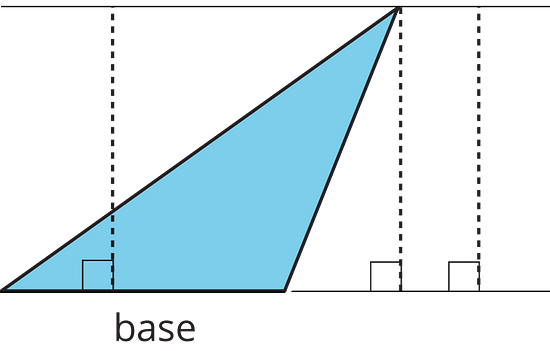
A segment showing a height must be drawn at a right angle to the base, but it can be drawn in more than one place. It does not have to go through the opposite vertex, as long as it connects the base and a line that is parallel to the base and goes through the opposite vertex, as shown here.

• Show Figure
  

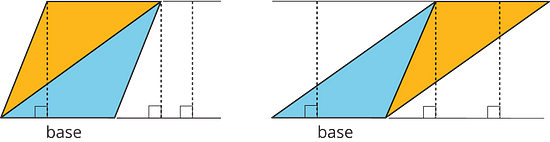
The base-height pairs in a triangle are closely related to those in a parallelogram. Recall that two copies of a triangle can be composed into one or more parallelograms. Each parallelogram shares at least one base with the triangle.

• Show Figures
  

For any base that they share, the corresponding height is also shared, as shown by the dashed segments.

We can use the base-height measurements and our knowledge of parallelograms to find the area of any triangle.

The formula for the area of a parallelogram with base b and height h is b · h.
A triangle takes up half of the area of a parallelogram with the same base and height. We can therefore express the area A of a triangle as: A = ½ · b · h.

• Show Figures
  

The area of Triangle A is 15 square units because ½ × 5 cm × 6 cm = 15 square cm.
The area of Triangle B is 4.5 square units because ½ × 3 cm × 3 cm = 4.5 square cm.
The area of Triangle C is 24 square units because ½ × 12 cm × 4 cm = 24 square cm.

In each case, one side of the triangle is the base but neither of the other sides is the height. This is because the angle between them is not a right angle.

• Show Figure
  

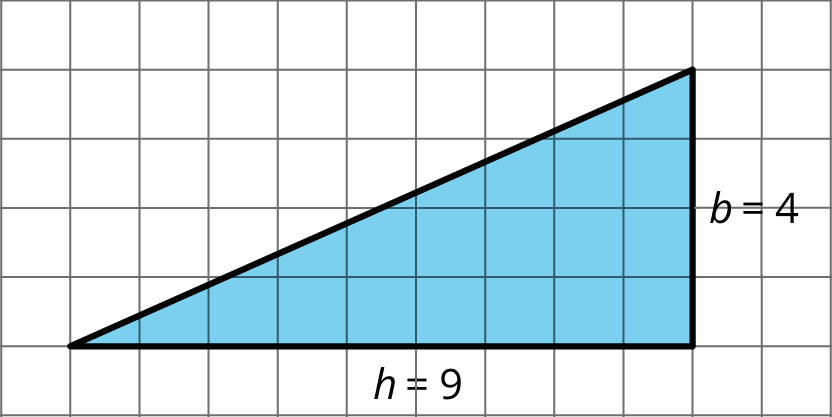
In right triangles, however, the two sides that are perpendicular can be a base and a height.

The area of this triangle is 18 square units whether we use 4 units or 9 units for the base.

Glossary Terms

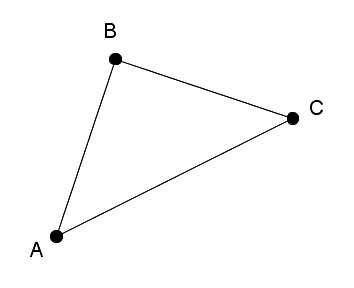
opposite vertex

For each side of a triangle, there is one vertex that is not on that side. This is the opposite vertex.

• Show Figure
  

For example, in this triangle, point A is the opposite vertex to side BC.

Practice Problems

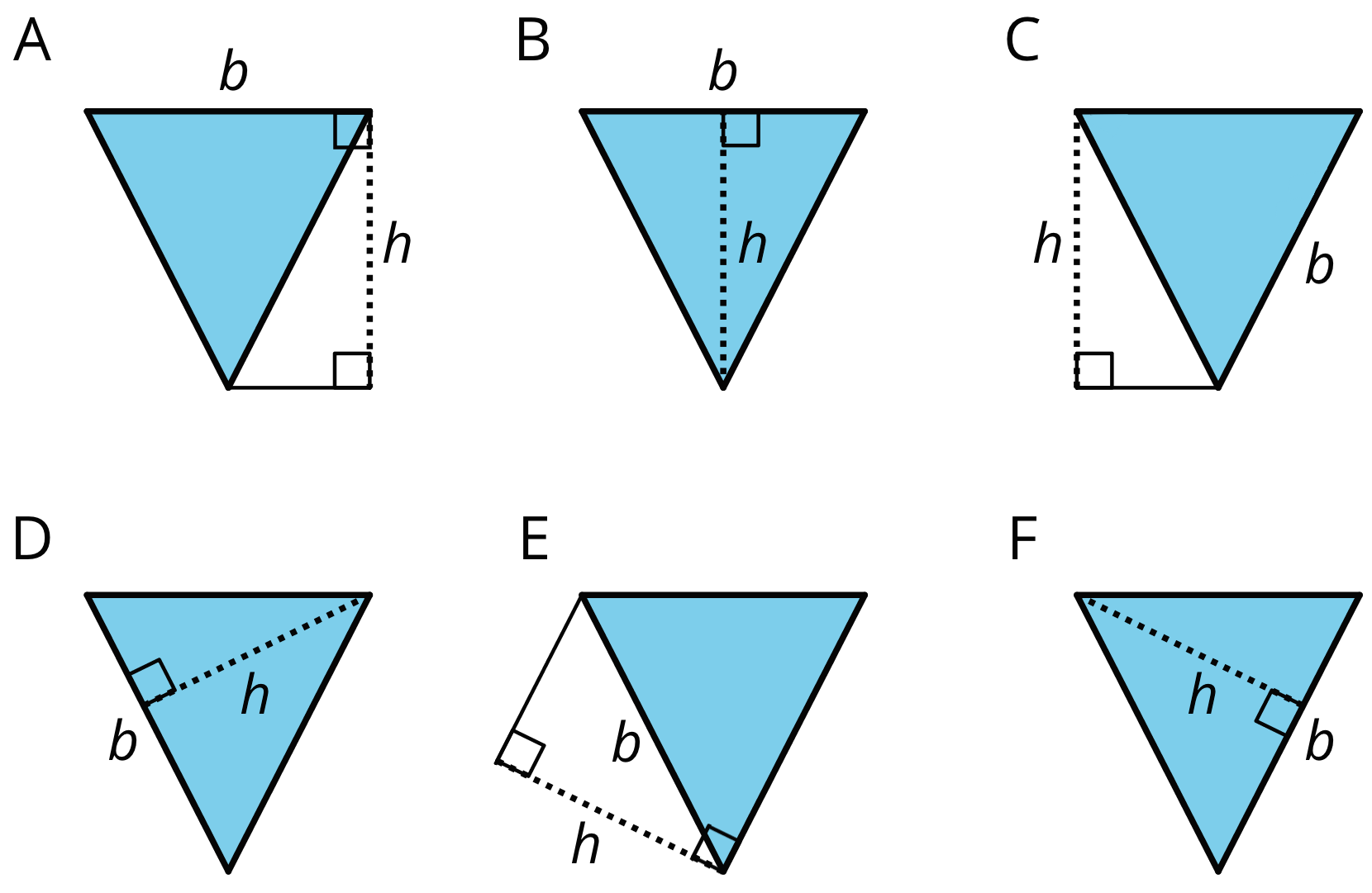
1. Select all drawings in which a corresponding height h for a given base b is correctly identified.

• Show Figures
  

• Answers

  A is correct. The height is perpendicular to the base and passes through a line parallel to the base which passes through the opposite vertex.

  B is correct. The height is perpendicular to the base and passes through the opposite vertex.
  C is incorrect. The labeled height is not perpendicular to the labeled base.
  D is correct.
  E is incorrect. The labeled height is not perpendicular to the labeled base.
  F is correct.

2. For each triangle, a base and its corresponding height are labeled.

• Show Figures
  

A: Find the area of each triangle.
B: How is the area related to the base and its corresponding height?

• Answers

  A: A = ½ · b · h
  Area of triangle A = ½ × 4 units × 6 units
  Area of triangle A = 12 square units
  Area of triangle B = ½ × 8 units × 4 units
  Area of triangle B = 16 square units
  Area of triangle C = ½ × 6 units × 4 units
  Area of triangle C = 12 square units

  B: The area is always half the product of the base and its corresponding height.

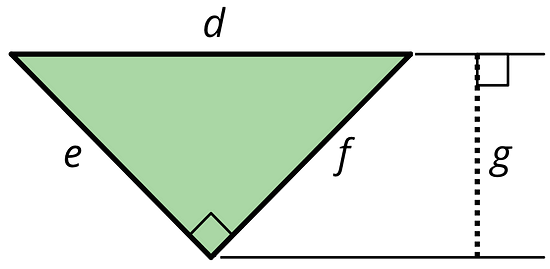
3. Here is a right triangle. Name a corresponding height for each base.

• Show Figures
  

A: Side d
B: Side e
C: Side f

• Answers

  A: Segment g is the corresponding height. It is perpendicular to side d and passes through a line that passes through the opposite vertex. Segment g is not a side of the triangle.
  B: Side f is perpendicular to side e and passes through the opposite vertex, so it can be the corresponding height.
  C: Side e is perpendicular to side f and passes through the opposite vertex, so it can be the corresponding height.

4. Find the area of the shaded triangle. Show your reasoning.

• Show Figures
  

• Answers

  The total area of the square is 6 × 6 = 36 square units.

  The area of the top unshaded triangle is ½ × 2 × 6 = 6 square units.
  The area of the bottom unshaded triangle is ½ × 4 × 6 = 12 square units.
  Hence, the area of the shaded triangle is 36 - 6 - 12 = 18 square units.

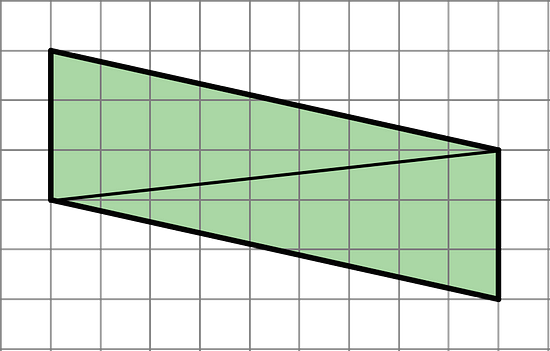
5. Andre drew a line connecting two opposite corners of a parallelogram. Select all true statements about the triangles created by the line Andre drew.

• Show Figures
  

A: Each triangle has two sides that are 3 units long.
B: Each triangle has a side that is the same length as the diagonal line.
C: Each triangle has one side that is 3 units long.
D: When one triangle is placed on top of the other and their sides are aligned, we will see that one triangle is larger than the other.
E: The two triangles have the same area as each other.

• Answers

  A is false.
  B is true.
  C is true.
  D is false. E is true. The two triangles created are each one half of the parallelogram.

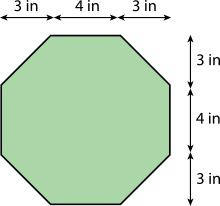
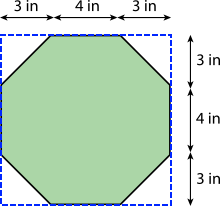
6. Here is an octagon.

• Show Figure
  

A: While estimating the area of the octagon, Lin reasoned that it must be less than 100 square inches. Do you agree? Explain your reasoning.
B: Find the exact area of the octagon. Show your reasoning.

• Answers
  

  A: Lin is correct. The octagon can be enclosed within a square that has an area of (3 + 4 + 3) in × (3 + 4 + 3) in = 100 square inches, as shown above. Since the octagon is this area minus the area of the unshaded corner triangles, the area of the octagon must be less than 100 square inches.
  B: The area of one of the unshaded corner triangles is ½ 3 in × 3 in = 4.5 square inches.
  The total area of all four triangles is 4.5 × 4 = 18 square inches.
  The area of the octagon is 100 square inches - 18 square inches = 82 square inches.

Try the free Mathway calculator and problem solver below to practice various math topics. Try the given examples, or type in your own problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.