The FOIL Method

The FOIL method is a mnemonic (a memory aid) used in algebra to help multiply two binomials. A binomial is a polynomial with two terms.

FOIL stands for
First
Outside
Inside
Last

It’s a systematic way to ensure that every term in the first binomial is multiplied by every term in the second binomial, which is essentially an application of the distributive property.

The following diagram shows how to use the FOIL method to distribute or multiply two binomials. Scroll down the page for more examples and solutions.

 

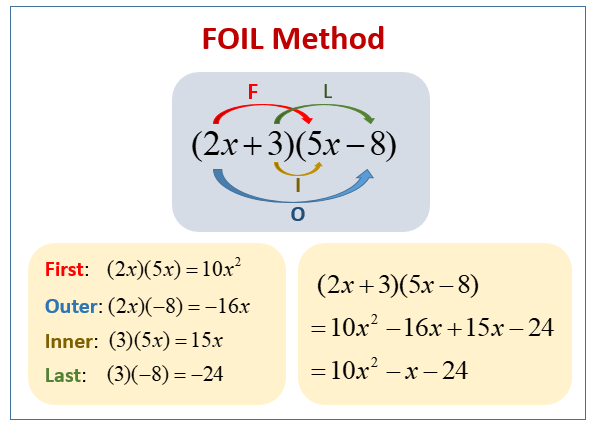
Important Notes:

• The FOIL method only works for multiplying two binomials. For more complex expressions, use the distributive property.
  
• After using FOIL, always check if you can simplify the resulting expression by combining like terms.
  

Algebra Worksheets
Practice your Algebra with the following worksheets.
Printable & Online Algebra Worksheets

Free Algebra Games
Distributive Property	Evaluate Algebraic Expressions	Evaluate Expressions (Exponents)
Simplify Algebraic Expressions	Solve Equations	Systems of Equations
Inequalities on the Number Line	Solve Inequalities	Multiply Binomials (y+b)(y+d)
Multiply Binomials (ay+b)(cy+d)	Solve Quadratic Equations

 

How the FOIL Method Works
Let’s take two general binomials: (a+b) and (c+d).

1. F - First: Multiply the first term of each binomial.
   a × c = ac
   

2. O - Outer: Multiply the two outermost terms (the first term of the first binomial and the last term of the second binomial).
   a × d = ad
   

3. I - Inner: Multiply the two innermost terms (the second term of the first binomial and the first term of the second binomial).
   b × c = bc
   

4. L - Last: Multiply the last term of each binomial.
   b × d = bd
   

After performing these four multiplications, you add the results together and then combine any like terms to simplify the expression.
So, (a+b)(c+d) = ac + ad + bc + bd.

Example:
Multiply the binomials (x + 1)(2x – 3)

Solution:
(x + 1)(2x – 3)

Multiply First : x • 2x = 2 x²
Multiply Outside : x • (–3) = –3x
Multiply Inside : 1 • 2x = 2x
Multiply Last : 1 • (–3) = –3

(x + 1)(2x – 3)
= 2x² – 3x + 2x – 3
= 2x² – x – 3

Multiplying Binomials FOIL Method
Multiplying binomials using the FOIL method. Explanation and examples.
(a + 3)(a + 7)
(x + 3)(x - 5)
(2x + 4)(3x + 5)

• Show Video

How to Use Foil to Distribute Two Binomials?
This video will show you how to use foil to distribute two binomials.
(x + 3)(x + 2)
(x + 4)(x - 5)
(x - 2)(x - 6)

• Show Video

FOIL Method for Multiplying Binomials - Distributive Property
In this video, we use the FOIL method to multiple binomials. FOIL helps you make sure all terms are distributed. (a+b)(c+d)
(x + 2)(3x - 7)

• Show Step-by-step Solutions

Practice Problems

1. Multiply (x+4)(x+5)
   Solution:
   (x+4)(x+5)= x² + 5x + 4x + 20 = x² + 9x + 20
   
2. Multiply (2x−3)(x+7)
   Solution:
   (2x−3)(x+7)=2x² + 14x − 3x − 21 = 2x² + 11x − 21
   
3. Multiply (3y+2)(y−4)
   Solution:
   (3y+2)(y−4)=3y² − 12y + 2y − 8 = 3y² − 10y − 8
   

Check out our most popular games!

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.